Modelleinstellungen: Unterschied zwischen den Versionen
| Zeile 159: | Zeile 159: | ||
Das spekulare Licht ist sozusagen der krönende Abschluss der Lichtberechnung. Jeder kennt die Glanzpunkte auf glatten Oberflächen (z.B. auf einer Billardkugel). Die Formel ähnelt der für diffuses Licht, allerdings streuen glatte Oberflächen weniger das Licht als stumpfe. Dadurch entsteht der bekannte Glanzpunkt. Mit dem Schieberegler können wir zunächst die Intensität des spekularen Lichtes bestimmen, um die Art des Materials (unbehandeltes Holz, Stein, Metall, Plastik, Glas usw.) auszudrücken. Die Standard-Einstellung des HomeNos liegt bei 0%. In diesem Fall wirken die Modelle absolut matt, weil der Dämpfungswert der Lichtstreuung extrem hoch ist. | Das spekulare Licht ist sozusagen der krönende Abschluss der Lichtberechnung. Jeder kennt die Glanzpunkte auf glatten Oberflächen (z.B. auf einer Billardkugel). Die Formel ähnelt der für diffuses Licht, allerdings streuen glatte Oberflächen weniger das Licht als stumpfe. Dadurch entsteht der bekannte Glanzpunkt. Mit dem Schieberegler können wir zunächst die Intensität des spekularen Lichtes bestimmen, um die Art des Materials (unbehandeltes Holz, Stein, Metall, Plastik, Glas usw.) auszudrücken. Die Standard-Einstellung des HomeNos liegt bei 0%. In diesem Fall wirken die Modelle absolut matt, weil der Dämpfungswert der Lichtstreuung extrem hoch ist. | ||
| + | |||
| + | |||
| + | <b><font size="4">V) Glanz (Lichtkonzentration des Glanzpunktes)</font></b> | ||
| + | |||
| + | Beim Eingabefeld des Glanzes haben wir es mit dem sogenannten Beleuchtungsexponent zu tun, dessen Wert zwischen 0 und 255 liegen kann. Die geometrische Wirkung des Exponenten kann man sich ungefähr so vorstellen: Je größer der Glanzexponent wird, desto kleiner und deutlicher wird der Glanzpunkt und desto glatter wirkt die Oberfläche. Allgemein kann man sagen: Je größer der Glanz wird, desto mehr Licht wird direkt zum Auge gespiegelt und nicht gestreut | ||
Version vom 7. Dezember 2016, 13:41 Uhr
5. Modelleinstellungen
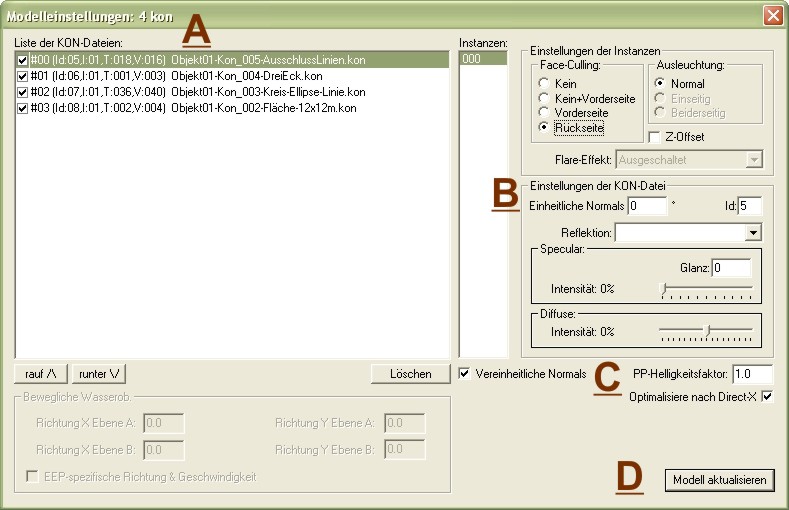
Über die Modelleinstellungen haben wir die Möglichkeit, Einstellungen und Parameter auf eine komplette *.kon-Datei anzuwenden. Im Dialog der Modelleinstellungen werden immer alle *.kon-Dateien angezeigt, die sich aktuell in unserem Objekt befinden. (vgl. Kapitel 2, Objekte). Die Modelleinstellungen rufen wir uns über die Schaltfläche ![]() in der oberen Leiste auf.
in der oberen Leiste auf.
A) Liste der KON-Dateien
Wie oben bereits erwähnt werden im Dialog der Modelleinstellungen stets alle .kon-Dateien angezeigt, welche sich aktuell in unserem Objekt befinden. Welche .kon-Datei gerade in unserem Objekt aktiv und somit im 3D-Betrachter zu sehen ist, erkennen wir am gesetzten Haken links neben der Bezeichnung unserer jeweiligen .kon-Datei.
Durch Herausnahme des Hakens mit der LMT deaktivieren wir unsere jeweilige .kon und schließen sie somit aus der 3D-Darstellung aus. Rechts neben dem schwarzen Häkchen sehen wir in chronologischer Reihenfolge folgende Informationen zur jeweiligen *.kon.
#00[fortlaufende Nummer]
Id:01[aktuell der .kon zugeordnete Id.-Nummer]
I:01[aktuelle Anzahl an Instanzen]
T:018[aktuelle Anzahl an Dreiecken (von englisch T=Triangle)]
V:016[aktuelle Anzahl an Vertexen (Einzelpunkten)]
"Objekt01-Kon_005-...." [aktueller Name der .kon-Datei]
Im Feld Instanzen können wir die Einstellungen der jeweiligen Unterinstanz unserer .kon aufrufen Die Verwendung der Taste "Strg" und der "Hochtaste" in Verbindung mit der LMT lassen uns mehrere .kon Dateien gleichzeitig auswählen und somit für Einstellungsänderungen aktivieren.
Das Z-Offset (z-Buffering)
Durch den Modus des Z-Offset wird garantiert, das Flächen, die sehr eng voreinander liegen, auch in größerer Entfernung immer noch in der richtigen Reihenfolge gezeichnet werden. D.h., dass z.B. Fenster vor der Hauswand bleiben und nicht ganz oder teilweise dahinter verschwinden.
Dabei muss die vorne liegende Fläche im Dialog "Modelleinstellungen" mit Z-Offset versehen werden.
<font size="4"B) Einstellungen der KON-Dateien
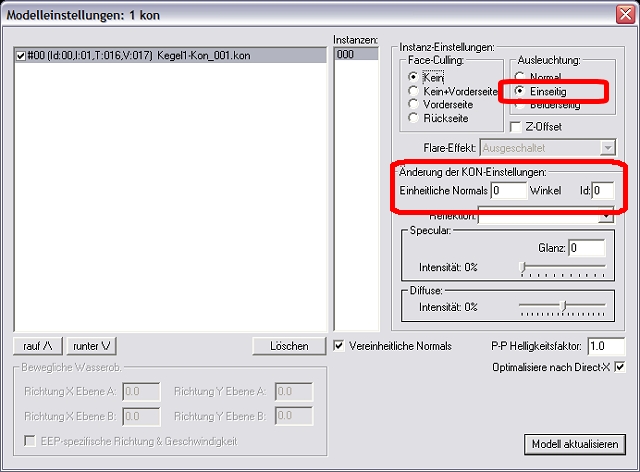
In "Einstellungen der KON-Dateien" sehen wir die Eingabefelder "Einheitliche Normals", "Id", "Reflektion", und Einstellungen zum spekularen und diffusen Licht. Gehen wir nun der Reihe nach auf die einzelnen Eingabemöglichkeiten ein.
I) Einheitliche Normals
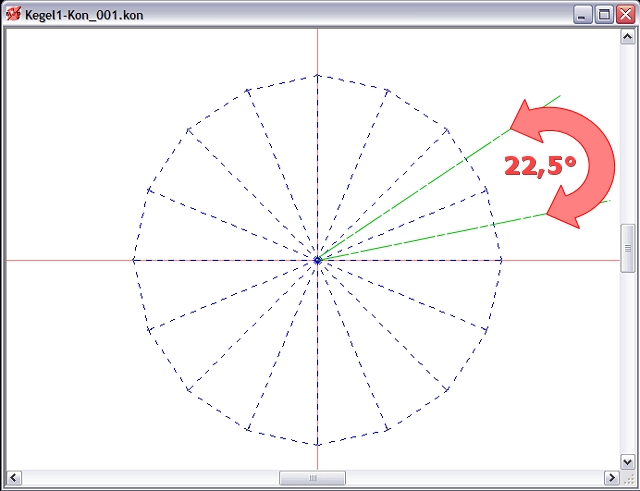
Unter "Einheitlich Normals" verstehen wir die Möglichkeit, Flächen, die in unseren .kon-Dateien in gewissen Winkeln zueinander stehen zu "vereinheitlichen" - d.h. die Winkel der einzelnen Konstrukte bzw...... Flächen innerhalb einer *.kon-Datei miteinander verrechnen zu lassen. Wir sehen uns dies nun an einem Beispiel an. In der Abb.1 sehen wir die Grundflächen eines Kegels bestehend aus 16 Außenflächen.
Abb.1: Kegel bestehend aus 16 einzelnen Dreiecken. Jedes Dreieck mit einem Öffnungswinkel von 22.5° ( 16 x[mal] 22.5° = 360°). Die Seitenlänge eines Dreiecks sei 100cm und die Höhe=h des Kegels im Mittelpunkt sei ebenfalls 100cm. Für den Kreis bekommen wir somit einen Durchmesser(d)von d=2 x r (Radius=Seitenlänge eines Dreiecks) = 2 x 100cm = 200cm.
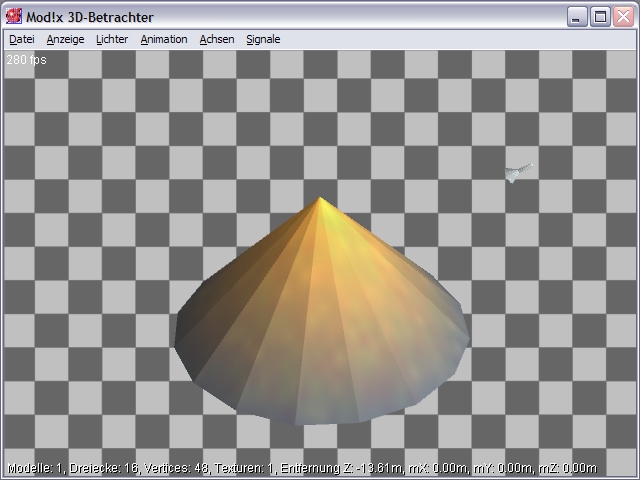
In der nachfolgenden 3D-Ansicht sehen wir nun die einzelnen Flächen (der Dreiecke), die die Form des Kegels bilden. Wir können hier noch nicht von einem runden Kegel, sondern vielmehr von einem kantigen Gebilde sprechen, das man als 16-seitige Pyramide bezeichnen könnte. Da die Normale der Dreiecke noch nicht vereinheitlicht wurden, behandelt die Grafikengine jedes einzelne Dreieck als eine absolut eigenständige geometrische Figur.
Abb.2: 3D-Ansicht des Kegels. Die Funktion "Einheitliche Normals" ist noch nicht aktiv, d.h. die Normals bzw. die Winkel werden noch nicht miteinander verrechnet bzw. vereinheitlicht.
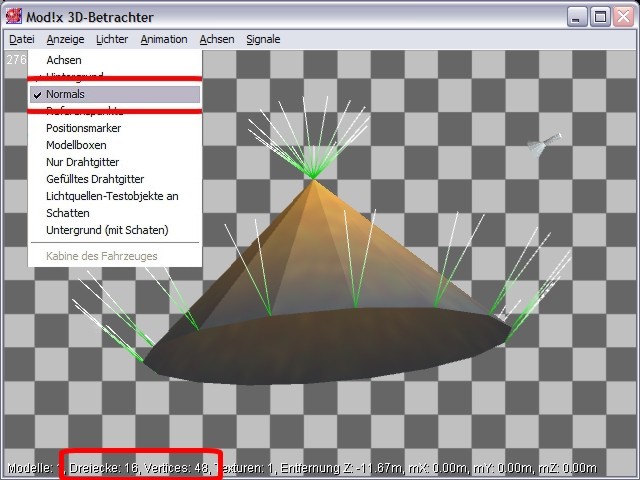
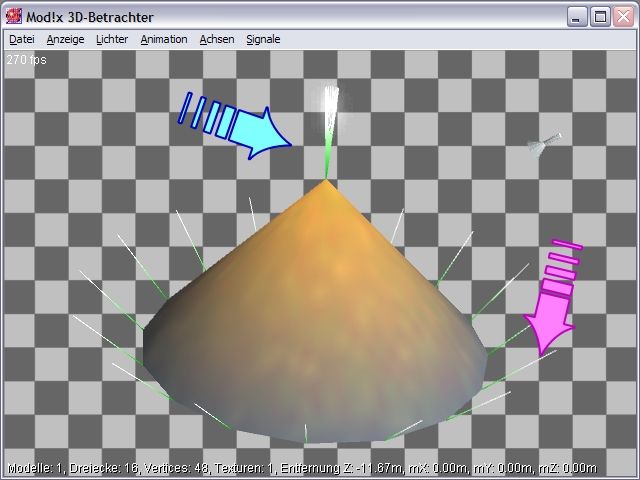
In der nächsten 3D-Ansicht sehen wir nun die Normalen eingeblendet und erkennen, daß sämtliche Normale einer jeweiligen Fläche in eine Richtung zeigen und somit innerhalb eines Dreiecks parallel zueinander stehen. Wir können zwar nicht alle Normale der Oberflächenpunkte sehen (dies würde auch keinen großen Sinn machen), dafür aber die Normale der Vertices (also der Eckpunkte der Dreiecke) anzeigen. Hierzu wird aus dem Menü des 3D-Betrachters "Anzeige-->Normals" ausgewählt.
Wenn wir uns die Normale des Kegels anschauen und durchzählen (man kann die angezeigten Normale verlängern, in dem die [SHIFT]- und die [F5]-Taste gleichzeitig gedrückt werden), so stellen wir fest, dass die Grafikengine tatsächlich 16 unabhängige Dreiecke mit insgesamt 48 Vertices berechnet, obwohl in der KON-Datei alle Dreiecke verbunden sind und in der Mitte einen gemeinsamen Vertex besitzen.
Es müssten demnach nur 17 Vertices sein! Was also geht hier vor?!
Abb.3: 3D-Ansicht des Kegels mit sichtbargemachten Normals. Der Öffnungswinkel zwischen den Normalen ist nun erkennbar, in welchem die 16 Dreiecke jeweils zueinander stehen.
Nun…, des Rätsels Lösung liegt in der Berechnungsart des Kegels, die in unserem Fall einseitig ist (und wir diese in unserem Tutorial weiterhin so belassen wollen).
Was heißt es aber konkret: eine einseitige Ausleuchtung"? Eine einseitige Ausleuchtung bedeutet, dass nur die Vorderseiten der Polygone auf das Licht reagieren und deren Rückseiten immer dunkel bleiben - auch für den Fall, dass die Lichtquelle so ausgerichtet ist, dass die Rückseiten bestrahl werden. Wann ist es der Fall? Nun, eigentlich ist es auch beim Kegel der Fall, weil ein typischer Kegel einen Boden, also eine Grundfläche besitz und von unten geschlossen ist. Ich habe den Boden aber absichtlich weggelassen, damit man in den Holraum des Kegels hineinschauen kann, ansonsten würden wir ja nicht sehen was im Inneren passiert. Da die "einseitige Ausleuchtung" erklärt wurde, sollten zugleich die anderen Arten der Ausleuchtung erklärt werden:
Eine "zweiseitige Ausleuchtung" bedeutet, dass sowohl die Au.enseiten, als auch die Innenseiten der Polygone auf das Licht reagieren. Dies funktioniert natärlich nur dann, wenn die Polygone beide Seiten besitzen, also nicht "backfacegecullt" sind. Diese Ausleuchtung eignet sich für alle offenen Flächen, die man sowohl von hinten, als auch von vorne betrachten kann. Ob das nun eine Gitterkonstruktion, ein Zaun, eine dünne Wand, oder ein Geländer ist - deren Konstruktion nur aus flachen Polygonen besteht – man kann sie alle von beiden Seiten betrachten und demnach auch beiderseitig ausleuchten.
Die dritte Art des Renderings heißt "Normal". Nun…, so ganz normal ist sie nicht und faktisch existiert sie im HomeNos nur deswegen, weil wir teilweise mit älteren Konstruktionen und Modellen zutun haben, die nicht nach der linkshändischen Formel gebaut wurden. Bei dieser Art der Ausleuchtung richtet sich das Licht nicht nach der Seite des Polygons (also vorne, oder hinten), vielmehr nach dessen Normalen. Das besondere dabei ist, dass wir (aufgrund der Bauweise der alten Modelle) der Grafikengine mitteilen können, dass sie – obwohl es sich eigentlich um die Rückseite des Polygons handelt – die Normale auf die gegenüberliegende Seite umlegen soll. Dabei werden die Normale umgepolt und sind auf der Rückseite zu sehen, obwohl sie laut der strengen Definition eines Normals dort nicht hingehören. (Die Vorderseite eines Polygons wird durch seinen Normal-Vektor bestimmt, drum kann man auch behaupten, dass wir in diesem Fall absichtlich gegen die Definition verstoßen – allerdings können wir dadurch Hunderte, wenn nicht Tausende von EEP-Konstruktionen retten...)
Nun kommen wir aber zu der eigentlichen Kuriosität: Warum haben wir plötzlich 48 anstatt 17 Vertices, wo man sie doch nachweislich abzählen kann? In der KON-Datei sind nur 17! Auch hierbei liegt der Grund in der möglichen (aber nicht korrekten) Bauweise der Modelle, bei der die Polygone nicht gedreht, sondern durch die Skalierung in der Z-Ebene um Minus Eins (-1) gestülpt werden können. Da die Normale der Dreiecke noch nicht normalisiert, also nicht vereinheitlicht wurden, so kann es durchaus passieren, dass eine KON-Datei (mit zwei, oder mehr Instanzen) Dreiecke aufweist, deren Normale (durch die Skalierung mit -1) in die "falsche" Richtung zeigen. Um dies herauszufinden, muss die Grafikengine jedes Dreieck einzeln abfragen und die Ausrichtung des Normalen untersuchen. Und hier fiel schon die konkrete Antwort: "Jedes Dreieck einzeln!"
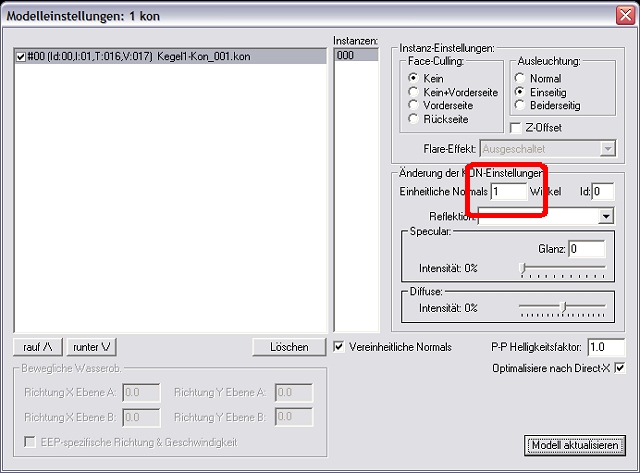
Da wir es mit 16 Dreiecken zutun haben, so müsste der Normalisierungsprozess bei 22,5. gut zu sehen sein, denn 360°/ 16 = 22,5. Nun, wir versuchen es aber mit einem kleineren Wert und schauen uns an, ob etwas passiert…
In der Tat, bereits bei der Eingabe von 1. fängt der Pixelshader damit an, die Dreiecke miteinander zu verrechnen und spätestens bei der Eingabe von 23. muss der Fall eintreten, dass die Normale im unteren Bereich des Kegels miteinander verschmelzen, also einen Durchschnitt der Ausleuchtung von zwei benachbarten Dreiecken bilden (es sind nach wie vor 48 Vertices).
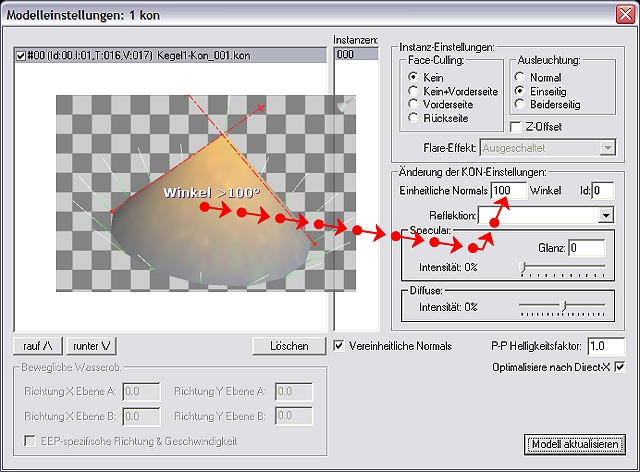
Unser Kegel sieht schon ganz rund aus, allerdings ist es uns noch nicht gelungen alle Normale des Kegels miteinander zu verrechnen, da der Winkel (23°) noch viel zu klein ist, damit die 16 Vertices an der Spitze einen Durchschnitt-Normal ergeben. Der Grund dafür liegt darin, dass wir bei unserem Kegel gegenüberliegende Dreiecke haben, deren Winkel zueinander etwas kleiner als 100° ist.
Wir rufen den Instanzen-Dialog auf und tragen beim Wert der Normal-Vereinheitlichung einen Winkel von 100°.
Durch die Winkelvereinheitlichung von 100° ist es uns endlich gelungen, sämtliche Normale des Kegels zu verschmelzen, womit an der Spitze nur noch ein, gemeinsamer Normal errechnet wird.
II) Id- Gruppenzuordnung
Im Feld Id können wir verschiedene *.kon-Dateien durch Vergabe derselben Identifikationsnummer einer gemeinsame Gruppen zuordnen. Gleiche Id`s vergeben wir in dem Fall, wenn mehrere *.kon-Dateien programmseitig als eine homogene Gruppe dargestellt und berechnet werden sollen. Nehmen wir als Bsp. an wir haben einen äußeren Kastenaufbau einer Lokomotive, der aus mehreren einzelnen *.kon-Dateien besteht. Für eine gute und einheitliche Darstellung des Kastenaufbaus möchten wir nun aber, daß die Einzel-*.kon`s programmseitig als eine, gemeinsame Datei behandelt werden. Um das zu erreichen versehen wir alle Einzel-*.kon-Dateien nun mit derselben Id-Nummer. Wir sehen uns dies nun an einem Beispiel an:
In den nachfolgenden Abbildungen sehen wir die 3D-Ansicht eines Kegels bestehend aus vier einzelnen .kon-Dateien
Abb.4.: Kegel ohne vereinheitlichte Normals und ohne einheitliche ID-Gruppen
Abb.5.: Kegel, gleiche ID-Gruppe (Id=200) vergeben an alle einzelnen .kon-Dateien des Würfels
Abb.6.: Kegel, gleiche ID-Gruppe (Id=200) vergeben an alle einzelnen .kon-Dateien des Würfels und Normals mit einem Winkel von 90Grad vereinheitlicht.
WICHTIG: Für Flächen nehmen wir für die Bildung von einheitlichen Id-Gruppen die Id = 200
III) Reflexion
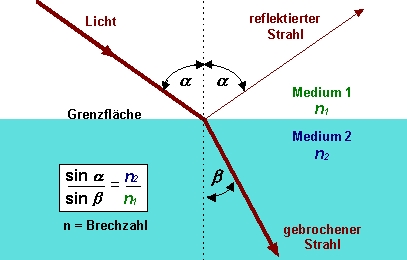
Das Phänomen der Reflexion lässt sich am anschaulichsten an einem Spiegel beobachten. Trifft Licht auf einen Spiegel (Medium 2), wird sämtliches Licht reflektiert, wobei der Einfallswinkel (α alpha) des Lichts immer dem Ausfallwinkel entspricht. Dies ist der Idealfall einer Reflexion, den wir in Abb.1 am Lichteinfallwinkel und reflektierten Strahl beobachten können. Trifft Licht nun auf ein flüssiges (z.B.Wasser) oder ein lichtdurchlässiges Medium (wie z.B. eine Fensterscheibe), wird der Lichtstrahl abgelenkt bzw. gebrochen. Wenn Licht auf Gegenstände trifft, die für unsere Augen farbig erscheinen, tritt noch ein anderes spezielleres Phänomen auf. Die Oberfläche eines z.B blauen Pigments absorbiert bestimmte Anteile des Lichts. Ein Teil des Lichts wird remittiert und in unserem System Auge-Gehirn entsteht der Farbeindruck Blau. Hier haben wir es mit dem Phänomen der Remission zu tun.
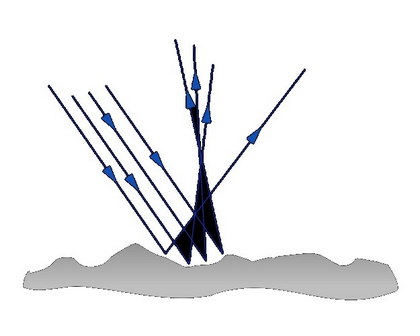
Abb.1: Gerichtete Reflexion (Licht - reflektierter Strahl) und Abb.2: Diffuse Reflexion auf rauhen Oberflächen
Lichtablenkung in Glas od. flüssigen Medien (gebrochener Strahl)
Die Intensität der Reflexion, also die Menge des remittierten Lichts hängt von dem Medium (Medium 2) ab auf die das Licht trifft. Grenzflächen mit einer großen Rauheit relativ zur Wellenlänge reflektieren diffus. Dies ist in Abb.2 dargestellt. Enthält das Material nun auch viele Streuzentren, folgt die Reflexion dem Lambertschen Gesetz. Die Hauptrückstreuung erfolgt dann senkrecht zum Material, unabhängig von der Einstrahlungsrichtung. Beispiele sind Milch, Wandfarbe oder Papier. Bei diesen Medien würden wir umgangssprachlich von komplett matten Gegenständen bzw. Materialien sprechen. Bei Milch haben die Fetttropfen im Wasser die Größenordnung der Wellenlänge des sichtbaren Lichtes und bilden die Streuzentren für Lichtwellen, gleiches gilt für die Lufteinschlüsse zwischen den Fasern bei Papier.
Werte der Reflexion im HomeNos
Wie wir eben besprochen haben, ist die Menge des reflektierten Lichts und somit die Intensität der Reflexion vom jeweiligen Medium abhängig, auf die der Lichtstrahl trifft. Des Weiteren haben wir gehört, daß Gegenstände bzw. Materialien, die eine rauhe Oberflächenstruktur aufweisen, den einfallenden Lichtstrahl diffus zurückwerfen bzw. reflektieren. Sehen wir uns nun an einem Beispiel an, wie sich die Einstellungen im HomeNos auf das Reflexionsverhalten unserer Modelle bzw. Objekte auswirken.
Im nachfolgenden Beispiel sehen wir ein Modell eines Fasses welches von 1 bis 4 mit verschiedenen Reflexionseinstellungen belegt wurde, die Werte sind für Glanz = 0 und Intensität =0.
Die Buchstaben M: M: E: stehen jeweils für die Werte M=Min: - M:=Max: - E:=Edging
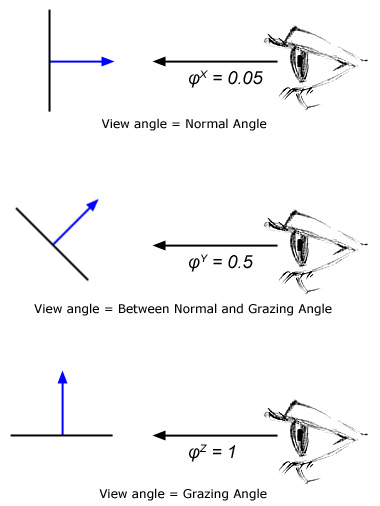
Reflektionswinkel:
Zuweisung der Reflektionswerte
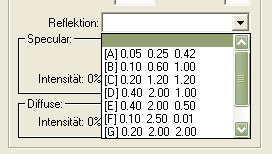
Im Auswahlfeld der "Reflektion" weisen wir unsere zuvor in den Grundeinstellungen vergebenen "Intensitätsstufen" (Min/Max/Edging) der Reflektion auf die ausgewählten .kon-Dateien zu:
IV) Specular [allgemein]
Das spekulare Licht ist sozusagen der krönende Abschluss der Lichtberechnung. Jeder kennt die Glanzpunkte auf glatten Oberflächen (z.B. auf einer Billardkugel). Die Formel ähnelt der für diffuses Licht, allerdings streuen glatte Oberflächen weniger das Licht als stumpfe. Dadurch entsteht der bekannte Glanzpunkt. Mit dem Schieberegler können wir zunächst die Intensität des spekularen Lichtes bestimmen, um die Art des Materials (unbehandeltes Holz, Stein, Metall, Plastik, Glas usw.) auszudrücken. Die Standard-Einstellung des HomeNos liegt bei 0%. In diesem Fall wirken die Modelle absolut matt, weil der Dämpfungswert der Lichtstreuung extrem hoch ist.
V) Glanz (Lichtkonzentration des Glanzpunktes)
Beim Eingabefeld des Glanzes haben wir es mit dem sogenannten Beleuchtungsexponent zu tun, dessen Wert zwischen 0 und 255 liegen kann. Die geometrische Wirkung des Exponenten kann man sich ungefähr so vorstellen: Je größer der Glanzexponent wird, desto kleiner und deutlicher wird der Glanzpunkt und desto glatter wirkt die Oberfläche. Allgemein kann man sagen: Je größer der Glanz wird, desto mehr Licht wird direkt zum Auge gespiegelt und nicht gestreut