G: Unterschied zwischen den Versionen
K (Schützte „G“ ([Bearbeiten=Nur Administratoren erlauben] (unbeschränkt) [Verschieben=Nur Administratoren erlauben] (unbeschränkt)) [kaskadierend]) |
|||
| Zeile 1: | Zeile 1: | ||
| + | <b><font size="4">Gammakorrektur</font></b> | ||
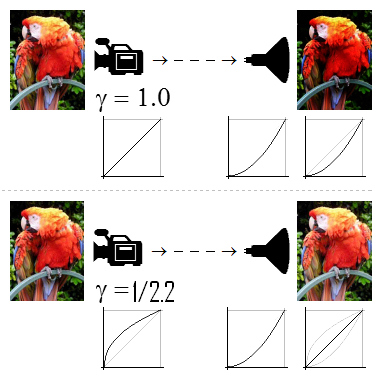
| − | + | <b>Gammakorrektur</b> ist eine namentlich im Bereich der Bildverarbeitung häufig verwendete Korrekturfunktion zur Überführung einer physikalisch proportional (d.h. linear) wachsenden Größe in eine dem menschlichen Empfinden gemäß nicht linear wachsende Größe. Die vom Menschen empfundene Helligkeit steigt in dunklen Bereichen steiler und in hellen weniger steil an. Die Stevenssche Potenzfunktion ordnet dem menschlichen Auge dabei ein Gamma von ca. 0,3 bis 0,5 zu. Soll das Helligkeitssignal eines linear arbeitenden Anzeigegerätes, beispielsweise eines Monitors, linear wahrgenommen werden, muss es daher mit dem reziproken des obigen Gammawerts (ca. 3,3 bis 2) vorverzerrt werden, damit sich beide Nichtlinearitäten für den Betrachter am Ende wieder aufheben. | |
| − | + | [[Datei:gamma_on_tv.jpg]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[http://wiki.eepshopping.de/index.php?title=Hauptseite_EEP_Wiki&redirect=no Zurück zur Startseite] | [http://wiki.eepshopping.de/index.php?title=Hauptseite_EEP_Wiki&redirect=no Zurück zur Startseite] | ||
Version vom 14. Dezember 2016, 13:03 Uhr
Gammakorrektur
Gammakorrektur ist eine namentlich im Bereich der Bildverarbeitung häufig verwendete Korrekturfunktion zur Überführung einer physikalisch proportional (d.h. linear) wachsenden Größe in eine dem menschlichen Empfinden gemäß nicht linear wachsende Größe. Die vom Menschen empfundene Helligkeit steigt in dunklen Bereichen steiler und in hellen weniger steil an. Die Stevenssche Potenzfunktion ordnet dem menschlichen Auge dabei ein Gamma von ca. 0,3 bis 0,5 zu. Soll das Helligkeitssignal eines linear arbeitenden Anzeigegerätes, beispielsweise eines Monitors, linear wahrgenommen werden, muss es daher mit dem reziproken des obigen Gammawerts (ca. 3,3 bis 2) vorverzerrt werden, damit sich beide Nichtlinearitäten für den Betrachter am Ende wieder aufheben.