M: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ [http://wiki.eepshopping.de/index.php?title=Hauptseite_EEP_Wiki&redirect=no Zurück zur Startseite]“) |
|||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | == Maleralgorithmus == | ||
| + | <b>Maleralgorithmus</b> ist eine einfache Lösung des Sichtbarkeitsproblems in der 3D-Computergrafik, das auch bei EEP eingesetzt wird. Bei der Darstellung einer dreidimensionalen Szene auf einer zweidimensionalen muss häufig entschieden werden, welche Polygone sichtbar und welche verdeckt sind. Der Name Maleralgorithmus ist eine <b>''Anspielung auf einen Maler, der die entfernten Objekte einer Szene zuerst zeichnet und sie dann mit den näher gelegenen übermalt''</b>. | ||
| + | <center>[[Datei:maleralgorithmus.jpg]]</center> | ||
| + | Entsprechend kann der Algorithmus in der Implementierung einer computergrafischen Anwendung eingesetzt werden: Zuerst werden alle Polygone ihrer Tiefe nach sortiert (Tiefensortierung, engl. depth sort) und dann werden sie der Reihenfolge nach gezeichnet. Durch das Überzeichnen der Bildanteile, die normalerweise nicht sichtbar sind, wird das Sichtbarkeitsproblem gelöst. Woran der Maleralgorithmus scheitert:<br> | ||
| + | Diese Verfahrensweise führt zu etlichen Problemen. Was passiert, wenn Polygon A teilweise Polygon B, B teilweise C und C wiederum teilweise A überschneidet? Es kann nicht mehr entschieden werden, welches Polygon vor welchem liegt. Ein ähnlicher Fall liegt vor, wenn sich zwei Polygone gegenseitig im dreidimensionalen Raum überschneiden. In solchen Fällen muss mindestens eines der betroffenen Polygone unterteilt werden, damit die Sortierung möglich ist und der Maleralgorithmus ein korrektes Ergebnis liefert. Ein anderes Problem ist, dass der Maleralgorithmus ineffizient ist, weil der Computer die Intensitäten aller Punkte eines Polygons berechnen muss, auch wenn das Polygon in der endgültigen Szene gar nicht sichtbar ist. Diese und andere Probleme mit dem Maleralgorithmus führten zur Entwicklung des [[Z|Z-Buffers]], der als logische Weiterentwicklung des Maleralgorithmus betrachtet werden kann. Durch die Verwendung eines Z-Buffers müssen die Objekte nicht mehr in der Reihenfolge ihrer Tiefe gerendert werden, was aber auch Probleme (z.B. mit Scheiben) verursachen kann. | ||
| + | == Material und Materialeigenschaften == | ||
| + | <b>Material bzw. Materialeigenschaften.</b> Ein natürliches Material wird in der 3D-Computergrafik entweder durch konstante Farbwerte oder Texturen definiert. Dabei sind einige Techniken unproblematisch echtzeitfähig, andere Verfahren sind bzw. waren durch die aufwändigen Berechnungen realistischen Renderprogrammen vorbehalten. Als echtzeitfähig, da sie im [[S|Gouraud Shading]] von den meisten Grafikkarten unterstützt werden, gelten folgende Materialeigenschaften:<br> | ||
| + | :•[[A|Ambient Lighting]] beschreibt die Objektfarbe durch einen konstanten Wert und simuliert die indirekte Beleuchtung durch die Umgebung.<br> | ||
| + | :•[[A|Diffuse Lighting]] beschreibt die Wirkung einer matten Oberfläche, von der das Licht gleichmäßig in alle Richtungen abgegeben wird.<br> | ||
| + | :•[[S|Specular Lighting]]: Dabei ist einstellbar, in welchem Winkelbereich, wie stark und in welcher Farbe ein Körper das Licht einer Lichtquelle reflektiert. Annähernd echt wirkende Reflexion wird durch eine Textur erzeugt, deren<br> Texturpunkte sich gemäß dem Reflexionsgesetz aus Betrachterpunkt und Oberflächennormalenvektor ergeben.<br> | ||
| + | :•[[A|Emissive Lighting]] beschreibt das Selbstleuchten von Objekten, wie zum Beispiel Lampen.<br> | ||
| + | :•Die [[A|Alpha Blending]] beschreibt die Durchsichtigkeit eines Materials.<br> | ||
| + | Als nicht echtzeitfähig (auch wenn sie von aktuellen Grafikkarten unterstützt werden und in diversen Spieln und Simulationen zunehmend eingesetzt werden) gelten:<br> | ||
| + | :•[[B|Bumpmapping]] bzw. Displacement Mapping beschreibt das Oberflächenrelief durch eine Textur.<br> | ||
| + | :•[[R|Reflexion]] wird entweder durch [[C|Reflection mapping (Cubemaps)]] oder durch Raytracing simuliert.<br> | ||
| + | :•Refraktion (Lichtbrechung) im Material.<br> | ||
| + | :•Kompliziertere Beleuchtungsmodelle.<br> | ||
| + | |||
| + | Die genauen Bezeichnungen können sich von Programm zu Programm ändern. Anzumerken ist, dass es sich bei den verwendeten Techniken um reine Nachbildungen visueller Effekte handelt, die nur die Illusion erwecken, es würden tatsächliche Lichteigenschaften nachgebildet. Tatsächlich ist es so, dass die verwendeten Algorithmen nur zu einem kleinen Teil tatsächlich auf physikalischen Verhaltensweisen von Licht in Interaktion mit Materie basieren. | ||
| + | |||
| + | |||
| + | == Mip Mapping == | ||
| + | |||
| + | <b>Mip Mapping</b> ist eine Antialiasing-Technik für Texturen. Sie wird in modernen 3D-Grafikchips zur Verbesserung der Bildqualität, aber auch der Geschwindigkeit eingesetzt. Das Problem beim [[U|Texture Mapping]] von Objekten besteht darin, dass man diese von nah und fern betrachten können soll. Korrelativ zum Erscheinungsbild des Objekts muss also auch die Textur ihre Form und Größe verändern:<br> | ||
| + | :•<b>Magnifikation</b> - die Textur muss stark vergrößert werden, um das Objekt zu bedecken, wenn es nah am Betrachter liegt.<br> | ||
| + | :•<b>Minifikation</b> - die Textur muss stark verkleinert werden, wenn das Objekt sehr weit vom Betrachter entfernt ist (im Extremfall ist das Objekt dann nur noch genau 1 Pixel groß)<br> | ||
| + | |||
| + | Werden keine Gegenmaßnahmen ergriffen, treten bei diesen Skalierungen Aliasing-Effekte auf, die als Artefakte sehr störend sind, besonders bei Mustern mit schrägen oder gerundeten Linien, als Verzerrungen oder Flimmern (Moiré-Effekte). | ||
| + | |||
| + | |||
| + | == MIP == | ||
| + | |||
| + | |||
| + | <b>MIP</b> ist eine Abkürzung für "<b>m</b>ultum <b>i</b>n <b>p</b>arvo", was soviel bedeutet wie "<b>''viel auf kleinem Platz''</b>". Eine MIP-Map (auch Bildpyramide) ist eine Folge von Rasterbildern desselben Motivs, jedoch mit abnehmender Auflösung. Die Kantenlänge jedes Bildes ist genau halb so groß wie die des Vorgängerbildes. Das kleinste Bild hat je nach Implementierung eine Größe von 1x1 oder 2x2 Pixel. Daraus folgt, dass alle Bilder als Kantenlänge eine 2er-Potenz haben müssen. MIP-Maps können einfach berechnet werden, indem für jedes Pixel des verkleinerten Bildes der Mittelwert der vier korrespondierenden Pixel des Ausgangsbildes berechnet wird. Dies ist rekursiv für alle weiteren Stufen durchzuführen. Dieses Verfahren wird häufig implizit von der Grafikhardware beim Texturladen angewandt, um Speicherbandbreite zu sparen. | ||
[http://wiki.eepshopping.de/index.php?title=Hauptseite_EEP_Wiki&redirect=no Zurück zur Startseite] | [http://wiki.eepshopping.de/index.php?title=Hauptseite_EEP_Wiki&redirect=no Zurück zur Startseite] | ||
Aktuelle Version vom 24. März 2017, 10:02 Uhr
Inhaltsverzeichnis
Maleralgorithmus
Maleralgorithmus ist eine einfache Lösung des Sichtbarkeitsproblems in der 3D-Computergrafik, das auch bei EEP eingesetzt wird. Bei der Darstellung einer dreidimensionalen Szene auf einer zweidimensionalen muss häufig entschieden werden, welche Polygone sichtbar und welche verdeckt sind. Der Name Maleralgorithmus ist eine Anspielung auf einen Maler, der die entfernten Objekte einer Szene zuerst zeichnet und sie dann mit den näher gelegenen übermalt.
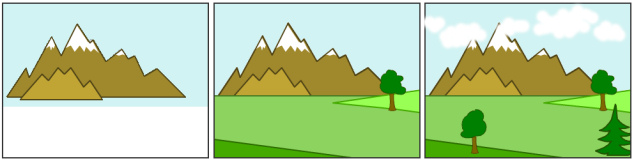
Entsprechend kann der Algorithmus in der Implementierung einer computergrafischen Anwendung eingesetzt werden: Zuerst werden alle Polygone ihrer Tiefe nach sortiert (Tiefensortierung, engl. depth sort) und dann werden sie der Reihenfolge nach gezeichnet. Durch das Überzeichnen der Bildanteile, die normalerweise nicht sichtbar sind, wird das Sichtbarkeitsproblem gelöst. Woran der Maleralgorithmus scheitert:
Diese Verfahrensweise führt zu etlichen Problemen. Was passiert, wenn Polygon A teilweise Polygon B, B teilweise C und C wiederum teilweise A überschneidet? Es kann nicht mehr entschieden werden, welches Polygon vor welchem liegt. Ein ähnlicher Fall liegt vor, wenn sich zwei Polygone gegenseitig im dreidimensionalen Raum überschneiden. In solchen Fällen muss mindestens eines der betroffenen Polygone unterteilt werden, damit die Sortierung möglich ist und der Maleralgorithmus ein korrektes Ergebnis liefert. Ein anderes Problem ist, dass der Maleralgorithmus ineffizient ist, weil der Computer die Intensitäten aller Punkte eines Polygons berechnen muss, auch wenn das Polygon in der endgültigen Szene gar nicht sichtbar ist. Diese und andere Probleme mit dem Maleralgorithmus führten zur Entwicklung des Z-Buffers, der als logische Weiterentwicklung des Maleralgorithmus betrachtet werden kann. Durch die Verwendung eines Z-Buffers müssen die Objekte nicht mehr in der Reihenfolge ihrer Tiefe gerendert werden, was aber auch Probleme (z.B. mit Scheiben) verursachen kann.
Material und Materialeigenschaften
Material bzw. Materialeigenschaften. Ein natürliches Material wird in der 3D-Computergrafik entweder durch konstante Farbwerte oder Texturen definiert. Dabei sind einige Techniken unproblematisch echtzeitfähig, andere Verfahren sind bzw. waren durch die aufwändigen Berechnungen realistischen Renderprogrammen vorbehalten. Als echtzeitfähig, da sie im Gouraud Shading von den meisten Grafikkarten unterstützt werden, gelten folgende Materialeigenschaften:
- •Ambient Lighting beschreibt die Objektfarbe durch einen konstanten Wert und simuliert die indirekte Beleuchtung durch die Umgebung.
- •Diffuse Lighting beschreibt die Wirkung einer matten Oberfläche, von der das Licht gleichmäßig in alle Richtungen abgegeben wird.
- •Specular Lighting: Dabei ist einstellbar, in welchem Winkelbereich, wie stark und in welcher Farbe ein Körper das Licht einer Lichtquelle reflektiert. Annähernd echt wirkende Reflexion wird durch eine Textur erzeugt, deren
Texturpunkte sich gemäß dem Reflexionsgesetz aus Betrachterpunkt und Oberflächennormalenvektor ergeben. - •Emissive Lighting beschreibt das Selbstleuchten von Objekten, wie zum Beispiel Lampen.
- •Die Alpha Blending beschreibt die Durchsichtigkeit eines Materials.
Als nicht echtzeitfähig (auch wenn sie von aktuellen Grafikkarten unterstützt werden und in diversen Spieln und Simulationen zunehmend eingesetzt werden) gelten:
- •Bumpmapping bzw. Displacement Mapping beschreibt das Oberflächenrelief durch eine Textur.
- •Reflexion wird entweder durch Reflection mapping (Cubemaps) oder durch Raytracing simuliert.
- •Refraktion (Lichtbrechung) im Material.
- •Kompliziertere Beleuchtungsmodelle.
Die genauen Bezeichnungen können sich von Programm zu Programm ändern. Anzumerken ist, dass es sich bei den verwendeten Techniken um reine Nachbildungen visueller Effekte handelt, die nur die Illusion erwecken, es würden tatsächliche Lichteigenschaften nachgebildet. Tatsächlich ist es so, dass die verwendeten Algorithmen nur zu einem kleinen Teil tatsächlich auf physikalischen Verhaltensweisen von Licht in Interaktion mit Materie basieren.
Mip Mapping
Mip Mapping ist eine Antialiasing-Technik für Texturen. Sie wird in modernen 3D-Grafikchips zur Verbesserung der Bildqualität, aber auch der Geschwindigkeit eingesetzt. Das Problem beim Texture Mapping von Objekten besteht darin, dass man diese von nah und fern betrachten können soll. Korrelativ zum Erscheinungsbild des Objekts muss also auch die Textur ihre Form und Größe verändern:
- •Magnifikation - die Textur muss stark vergrößert werden, um das Objekt zu bedecken, wenn es nah am Betrachter liegt.
- •Minifikation - die Textur muss stark verkleinert werden, wenn das Objekt sehr weit vom Betrachter entfernt ist (im Extremfall ist das Objekt dann nur noch genau 1 Pixel groß)
Werden keine Gegenmaßnahmen ergriffen, treten bei diesen Skalierungen Aliasing-Effekte auf, die als Artefakte sehr störend sind, besonders bei Mustern mit schrägen oder gerundeten Linien, als Verzerrungen oder Flimmern (Moiré-Effekte).
MIP
MIP ist eine Abkürzung für "multum in parvo", was soviel bedeutet wie "viel auf kleinem Platz". Eine MIP-Map (auch Bildpyramide) ist eine Folge von Rasterbildern desselben Motivs, jedoch mit abnehmender Auflösung. Die Kantenlänge jedes Bildes ist genau halb so groß wie die des Vorgängerbildes. Das kleinste Bild hat je nach Implementierung eine Größe von 1x1 oder 2x2 Pixel. Daraus folgt, dass alle Bilder als Kantenlänge eine 2er-Potenz haben müssen. MIP-Maps können einfach berechnet werden, indem für jedes Pixel des verkleinerten Bildes der Mittelwert der vier korrespondierenden Pixel des Ausgangsbildes berechnet wird. Dies ist rekursiv für alle weiteren Stufen durchzuführen. Dieses Verfahren wird häufig implizit von der Grafikhardware beim Texturladen angewandt, um Speicherbandbreite zu sparen.