Arbeit mit .kon-Dateien: Unterschied zwischen den Versionen
HW1 (Diskussion | Beiträge) |
|||
| (14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Datei:Redaktioneller_Hinweis.png]] | ||
<b><font size="4">3. Arbeiten mit .kon-Dateien</font></b> | <b><font size="4">3. Arbeiten mit .kon-Dateien</font></b> | ||
| − | Haben wir unser neu erstelltes Objekt aufgerufen und ist es aktiv wollen wir in das Modellieren selbst einsteigen. Ein Objekt besteht immer aus einer Untergruppe von | + | Haben wir unser neu erstelltes Objekt aufgerufen und ist es aktiv wollen wir in das Modellieren selbst einsteigen. Ein Objekt besteht immer aus einer Untergruppe von sogenannten .kon-Dateien. Dies sind 2D Konstruktionsdateien, in welchen wir die Geometrie des Objektes zeichnen. Eine neue *.kon-Datei legen wir an, indem wir auf das Symbol [[Datei:4_neue-kon-datei.jpg]] auf unserer oberen Schaltfläche klicken.Es erscheint ein Fenster mit einem roten Koordinatensystem und der Bezeichnung unseres Objektnamens mit dem Zusatz „…-Kon_001.kon“. Wir maximieren uns das Fenster um nun mit mehr Übersicht arbeiten zu können. |
Die KON-Datei ist für uns am Anfang das wichtigste Element für die Konstruktion von Modellen. Hier zeichnen wir die darzustellenden Flächen und legen ihre Position im 3D Raum fest. Wichtig ist, das wir immer geschlossene Formen zeichnen, und gewisse Regeln einhalten. | Die KON-Datei ist für uns am Anfang das wichtigste Element für die Konstruktion von Modellen. Hier zeichnen wir die darzustellenden Flächen und legen ihre Position im 3D Raum fest. Wichtig ist, das wir immer geschlossene Formen zeichnen, und gewisse Regeln einhalten. | ||
| Zeile 47: | Zeile 48: | ||
Wir beginnen mit einer einfachen geometrischen Figur dem Rechteck, und klicken hierfür auf die Schaltfläche mit dem Symbol [[Datei:img_15.jpg]]. An unserem Mauszeiger öffnet sich ein offenes Rechtecksymbol. Dies zeigt uns an, dass wir nun mit dem Zeichen beginnen können und wir tun dies gleich, indem wir nach einem Druck auf die linke Maustaste (LMT) das Rechteck beliebig nach allen Seiten im Koordinatensystem aufziehen. | Wir beginnen mit einer einfachen geometrischen Figur dem Rechteck, und klicken hierfür auf die Schaltfläche mit dem Symbol [[Datei:img_15.jpg]]. An unserem Mauszeiger öffnet sich ein offenes Rechtecksymbol. Dies zeigt uns an, dass wir nun mit dem Zeichen beginnen können und wir tun dies gleich, indem wir nach einem Druck auf die linke Maustaste (LMT) das Rechteck beliebig nach allen Seiten im Koordinatensystem aufziehen. | ||
| − | [[Datei:3.1_rechteckansicht_homenos-recduced.jpg]] | + | <center>[[Datei:3.1_rechteckansicht_homenos-recduced.jpg]]</center> |
Es erscheint der Dialog für die geometrische Figur des Rechtecks: | Es erscheint der Dialog für die geometrische Figur des Rechtecks: | ||
| − | [[Datei:3.1_rechteckdialog_homenos_mit-beschr.jpg]] | + | <center>[[Datei:3.1_rechteckdialog_homenos_mit-beschr.jpg]]</center> |
| − | Die <b>Pos.X</b> und <b>Pos.Y</b> (Pos.=Position) bestimmen die Lage unserer geometrischen Figur in Abhängigkeit zum Nullpunkt (x=0 /y=0) unseres Koordinatensystems. Im Falle des Rechtecks beziehen sich die dortigen Eingaben auf den linken oberen Punkt,den sogenannten <b>Null-Vertex</b> (oder auch Nullpunkt) unserer geometrischen Figur. In den Eingabefeldern Länge und Höhe definieren wir die Ausmaße unseres Rechtecks. Im oberen Beispiel erkennen wir die Eingaben Länge=1200 und Höhe=1000. Da die Eingaben in der Maßeinheit Zentimeter erkannt werden, erhalten wir somit ein Rechteck mit einer Länge von 12 Metern und einer Höhe von 10 Metern. Die Eingabefelder Textur X/Y und die zugehörigen Felder Länge und Höhe geben uns die Möglichkeit unsere erstellten Texturen/Bilddateien auf unserer geometrische Figur aufzubringen. Im Feld Textur-ID tragen wir die entsprechende Nummer bzw. id der Textur ein, welche wir später auf unser Konstrukt aufbringen möchte. | + | Die <b>Pos.X</b> und <b>Pos.Y</b> (Pos.=Position) bestimmen die Lage unserer geometrischen Figur in Abhängigkeit zum Nullpunkt (x=0 /y=0) unseres Koordinatensystems. Im Falle des Rechtecks beziehen sich die dortigen Eingaben auf den linken oberen Punkt, den sogenannten <b>Null-Vertex</b> (oder auch Nullpunkt) unserer geometrischen Figur. In den Eingabefeldern Länge und Höhe definieren wir die Ausmaße unseres Rechtecks. Im oberen Beispiel erkennen wir die Eingaben Länge=1200 und Höhe=1000. Da die Eingaben in der Maßeinheit Zentimeter erkannt werden, erhalten wir somit ein Rechteck mit einer Länge von 12 Metern und einer Höhe von 10 Metern. Die Eingabefelder Textur X/Y und die zugehörigen Felder Länge und Höhe geben uns die Möglichkeit unsere erstellten Texturen/Bilddateien auf unserer geometrische Figur aufzubringen. Im Feld Textur-ID tragen wir die entsprechende Nummer bzw. id der Textur ein, welche wir später auf unser Konstrukt aufbringen möchte. |
Bestätigen wir unsere Eingaben mit OK erhalten wir folgende geometrische Figur. Zusätzlich öffnen wir in der Ansicht mit einem Doppelklick des Buttons [[Datei:img_22.jpg]] auf den linken oberen Punkt unseren sogenannten Vertex-Dialog für eben den oberen linken Punkt (Vertex). Abgebildet sehen wir den Dialog in der oberen Grafik unter <b>"Eigenschaften von Vertex:0"</b>. Wie wir an den Eigenschaften des Vertex(e) erkennen können hat unser Rechteck genau die vorher im Dialog eingestellten Ausmaße. Der bereits aufgerufenen Null-Vertex liegt in der Horizontale bei x=600 und in der Vertikale bei Y=-1000. Analog dazu werden wir beim Aufrufen der Eigenschaften des rechten, oberen Vertex die Koordinaten x=-600 und y=-1000 vergeben sehen. Die beiden unteren Vertexe liegen auf der X-Achse und haben somit beide die y-Werte = 0. In x-Ausrichtung sehen wir analog zu den beiden oberen Vertexen die Werte x=600 und x=-600. Dank der beiden Eingaben der Pos.X = -600 und der Pos.Y =-1000 liegt unser Rechteck in der Mitte der x-Achse und mit den beiden unteren Vertexen auf der y-Achse auf. (vgl. Pos.X/ Pos.Y in "Einstellung Rechteck") | Bestätigen wir unsere Eingaben mit OK erhalten wir folgende geometrische Figur. Zusätzlich öffnen wir in der Ansicht mit einem Doppelklick des Buttons [[Datei:img_22.jpg]] auf den linken oberen Punkt unseren sogenannten Vertex-Dialog für eben den oberen linken Punkt (Vertex). Abgebildet sehen wir den Dialog in der oberen Grafik unter <b>"Eigenschaften von Vertex:0"</b>. Wie wir an den Eigenschaften des Vertex(e) erkennen können hat unser Rechteck genau die vorher im Dialog eingestellten Ausmaße. Der bereits aufgerufenen Null-Vertex liegt in der Horizontale bei x=600 und in der Vertikale bei Y=-1000. Analog dazu werden wir beim Aufrufen der Eigenschaften des rechten, oberen Vertex die Koordinaten x=-600 und y=-1000 vergeben sehen. Die beiden unteren Vertexe liegen auf der X-Achse und haben somit beide die y-Werte = 0. In x-Ausrichtung sehen wir analog zu den beiden oberen Vertexen die Werte x=600 und x=-600. Dank der beiden Eingaben der Pos.X = -600 und der Pos.Y =-1000 liegt unser Rechteck in der Mitte der x-Achse und mit den beiden unteren Vertexen auf der y-Achse auf. (vgl. Pos.X/ Pos.Y in "Einstellung Rechteck") | ||
| Zeile 59: | Zeile 60: | ||
Im <b>3D-Betrachter</b> erhalten wir zu unserem Rechteck folgende Ansicht: | Im <b>3D-Betrachter</b> erhalten wir zu unserem Rechteck folgende Ansicht: | ||
| − | [[Datei:3.1_rechteckansicht-3d_homenos.jpg]] | + | <center>[[Datei:3.1_rechteckansicht-3d_homenos.jpg]]</center> |
Nun lassen sich unsere Eingaben im Rechteckdialog anschaulich nachvollziehen. Wir erkennen, daß auf unserem Rechteck aktuell die gesamte Textur von x=0 (genau:0.0005) bis x=1 (0.9990)und von y=0 (genau:0.0005) bis y=1 (0.9990) aufgetragen ist.(<b>vgl. hierzu "Einstellung Rechteck"</b> Textur x/y, Länge/Höhe). Die genauen Werte sind an dieser Stelle wichtig, da wir ein Textur niemals direkt bis an Ihren Rand auftragen sollten.Würden wir dies tun entstünden an den Rändern unseres Rechtecks weiße, untexturierte Flächen. Die Informationen am unteren Rand unseres 3-D Betrachters liefern uns die aktuelle Anzahl an Dreiecken (in diesem Fall 2). Denn Zeichnen wir ein geometrische Figur wie hier das Rechteck, wird es uns auch als Rechteck dargestellt, intern allerdings immer in die kleinste geometrische Einheit - d.h in Dreiecke aufgeteilt. Weiter wird uns die Anzahl an Vertexen/ Einzelpunkten = 4 angezeigt und die Anzahl an bereits verwendeten Texturen für unser Modell (aktuell = 1). Die Entfernungswerte informieren uns immer über den aktuellen Sichtabstand in unserer 3D-Ansicht. | Nun lassen sich unsere Eingaben im Rechteckdialog anschaulich nachvollziehen. Wir erkennen, daß auf unserem Rechteck aktuell die gesamte Textur von x=0 (genau:0.0005) bis x=1 (0.9990)und von y=0 (genau:0.0005) bis y=1 (0.9990) aufgetragen ist.(<b>vgl. hierzu "Einstellung Rechteck"</b> Textur x/y, Länge/Höhe). Die genauen Werte sind an dieser Stelle wichtig, da wir ein Textur niemals direkt bis an Ihren Rand auftragen sollten.Würden wir dies tun entstünden an den Rändern unseres Rechtecks weiße, untexturierte Flächen. Die Informationen am unteren Rand unseres 3-D Betrachters liefern uns die aktuelle Anzahl an Dreiecken (in diesem Fall 2). Denn Zeichnen wir ein geometrische Figur wie hier das Rechteck, wird es uns auch als Rechteck dargestellt, intern allerdings immer in die kleinste geometrische Einheit - d.h in Dreiecke aufgeteilt. Weiter wird uns die Anzahl an Vertexen/ Einzelpunkten = 4 angezeigt und die Anzahl an bereits verwendeten Texturen für unser Modell (aktuell = 1). Die Entfernungswerte informieren uns immer über den aktuellen Sichtabstand in unserer 3D-Ansicht. | ||
| Zeile 71: | Zeile 72: | ||
<b>In der 2D Ansicht erhalten wir nun für einen Kreis folgende Darstellung:</b> | <b>In der 2D Ansicht erhalten wir nun für einen Kreis folgende Darstellung:</b> | ||
| − | [[Datei:hmfile_hash_ba4c5f23.jpg]] | + | <center>[[Datei:hmfile_hash_ba4c5f23.jpg]]</center> |
<b>und folgende Darstellung für eine Ellipse bzw. Linie:</b> | <b>und folgende Darstellung für eine Ellipse bzw. Linie:</b> | ||
| − | [[Datei:hmfile_hash_b0d8957f.jpg]] | + | <center>[[Datei:hmfile_hash_b0d8957f.jpg]]</center> |
| − | Und hier unsere 2D-Zeichnung im 3D-Betrachter. Wir erkennen unseren Kreis und die Ellipse. Und bemerken, | + | Und hier unsere 2D-Zeichnung im 3D-Betrachter. Wir erkennen unseren Kreis und die Ellipse. Und bemerken, dass unsere Linie nicht sichtbar ist. Dies rührt daher, dass sie wie oben beschrieben über keine eigenen Einzelpunkte verfügt. Würde man unsere Linie nun nachträglich mit Vertexen/Punkten versehen, erhielten wir allerdings ebenfalls (noch) keine 3D Darstellung, da eine einfache Linie weder über eine 2D Fläche noch über ein 3D-Volumen verfügt. |
| − | [[Datei:hmfile_hash_cccfdc50.jpg]] | + | <center>[[Datei:hmfile_hash_cccfdc50.jpg]]</center> |
| Zeile 88: | Zeile 89: | ||
Über den Vertexdialog [[Datei:img_22.jpg]] lassen sich die Lage des Vertexes im Raum (Koordinaten x,y,z), seine Grundfarbe (Farbwerte unbelechtet), Lichteinstellungen (Farbwerte beleuchtet), die Reflektionseinstellungen (Reflektion&Emitting) und die spekularen Lichteinstellungen (Specular) setzen. Über den Bereich "Textur" im Vertexdialog haben wir die Möglichkeit die Lage des Vertexes auf unserer Textur in x und y Richtung zu bestimmen. Ferner haben wir die Möglichkeit ein Bloom-Faktor zu vergeben. | Über den Vertexdialog [[Datei:img_22.jpg]] lassen sich die Lage des Vertexes im Raum (Koordinaten x,y,z), seine Grundfarbe (Farbwerte unbelechtet), Lichteinstellungen (Farbwerte beleuchtet), die Reflektionseinstellungen (Reflektion&Emitting) und die spekularen Lichteinstellungen (Specular) setzen. Über den Bereich "Textur" im Vertexdialog haben wir die Möglichkeit die Lage des Vertexes auf unserer Textur in x und y Richtung zu bestimmen. Ferner haben wir die Möglichkeit ein Bloom-Faktor zu vergeben. | ||
| − | [[Datei:3.1.3_einzelvertexe.jpg]] | + | <center>[[Datei:3.1.3_einzelvertexe.jpg]]</center> |
In den <b>Eigenschaften</b> (Vertexdialog) unseres Punktes lassen sich sogleich folgende Einstellungen erkennen: | In den <b>Eigenschaften</b> (Vertexdialog) unseres Punktes lassen sich sogleich folgende Einstellungen erkennen: | ||
| Zeile 100: | Zeile 101: | ||
Kommen wir nun aber zurück zur eigentlichen Konstruktionsarbeit mit Vertexen. Im oberen Schaubild sehen wir eine Dreieckskonstruktion. Diese geometrische Figur erstellen wir in dem wir 3 Einzelvertexe an unseren gewünschten Punkten im Koordinatensystem setzen und sie anschließend mit der [[Datei:img_12.jpg]] Unterteilungs- /Verbindungslinie verbinden. Im 3D-Betrachter erhalten wir folgende Darstellung: | Kommen wir nun aber zurück zur eigentlichen Konstruktionsarbeit mit Vertexen. Im oberen Schaubild sehen wir eine Dreieckskonstruktion. Diese geometrische Figur erstellen wir in dem wir 3 Einzelvertexe an unseren gewünschten Punkten im Koordinatensystem setzen und sie anschließend mit der [[Datei:img_12.jpg]] Unterteilungs- /Verbindungslinie verbinden. Im 3D-Betrachter erhalten wir folgende Darstellung: | ||
| − | [[Datei:3.1.3_einzelvertexe-dreieck-3d.jpg]] | + | <center>[[Datei:3.1.3_einzelvertexe-dreieck-3d.jpg]]</center> |
| Zeile 113: | Zeile 114: | ||
| − | [[Datei:3.1.4_ausschlusslinie.jpg]] | + | <center>[[Datei:3.1.4_ausschlusslinie.jpg]]</center> |
...in unserer 3D-Ansicht ist der Unterschied für uns sofort gut erkennbar: | ...in unserer 3D-Ansicht ist der Unterschied für uns sofort gut erkennbar: | ||
| − | [[Datei:3.1.4_ausschlusslinie-3d.jpg]] | + | <center>[[Datei:3.1.4_ausschlusslinie-3d.jpg]]</center> |
Abb.: Instanzebene der *.kon-Datei | Abb.: Instanzebene der *.kon-Datei | ||
| Zeile 129: | Zeile 130: | ||
Den Dialog jeder einzelnen *.kon-Datei rufen wir uns über das Symbol [[Datei:img_23.jpg]] auf. Wir erhalten dann folgende Ansicht: | Den Dialog jeder einzelnen *.kon-Datei rufen wir uns über das Symbol [[Datei:img_23.jpg]] auf. Wir erhalten dann folgende Ansicht: | ||
| − | [[Datei:3.2.instanztebene-lage-d-instebene.jpg]] | + | <center>[[Datei:3.2.instanztebene-lage-d-instebene.jpg]]</center> |
<b>Abb.:</b> Instanzebene der *.kon-Datei | <b>Abb.:</b> Instanzebene der *.kon-Datei | ||
| Zeile 136: | Zeile 137: | ||
<b><font size="4">3.2.1 Lage im Koordinatensystem</font></b> | <b><font size="4">3.2.1 Lage im Koordinatensystem</font></b> | ||
| − | Nachfolgend sehen wir die <b>Ausgangslage</b> eines Konstrukts einer .kon-Datei im Koordinatensystem. Ausgangslage bedeutet, | + | Nachfolgend sehen wir die <b>Ausgangslage</b> eines Konstrukts einer .kon-Datei im Koordinatensystem. Ausgangslage bedeutet, dass das Konstrukt nach Erstellung noch keine weiteren Parameter als die automatisch eingestellte Ausgangsdrehung erhalten hat. Die Ausgangsdrehung von 270° (= -90°) ist in der Grafik gut ersichtlich. Die Achse um die primär, neben der automatischen Aufstellung um die x-Achse von -90°/ 270°, gedreht wird ist die z-Achse. So würden z.B. die Seiten des in der Abbildung zu sehenden Hauses um -90° bzw. +90° um die z-Achse gedreht. Natürlich gibt es hier von Modell zu Modell Unterschiede. Als Ausgangspunkt ist es gut sich immer hier gezeigte Ausgangslage anzusehen bzw. vorzustellen, und von dort aus Schritt für Schritt die Drehungen um die x,y, und z-Achsen vorzunehmen, bis die gewünschten Lage des Konstrukts im Raum erreicht ist. |
<b>Siehe hierzu auch Kapitel:</b> <b><font color="blue">Normen und Maßvorgaben (Lage der Modelle)</font></b> | <b>Siehe hierzu auch Kapitel:</b> <b><font color="blue">Normen und Maßvorgaben (Lage der Modelle)</font></b> | ||
| − | [[Datei:3_aa_koordinaten-dialog-3d_2.jpg]] | + | <center>[[Datei:3_aa_koordinaten-dialog-3d_2.jpg]]</center> |
<b>Abb.: 3D-Ansicht der Lage einer .kon-Datei mit Ausgangsdrehung 270° im Koordinatensystem</b> | <b>Abb.: 3D-Ansicht der Lage einer .kon-Datei mit Ausgangsdrehung 270° im Koordinatensystem</b> | ||
| Zeile 147: | Zeile 148: | ||
<b>Erklärungen zu den Einstellungen in den Instanzen</b> | <b>Erklärungen zu den Einstellungen in den Instanzen</b> | ||
| − | Gehen wir nun etwas genauer auf die Einstellungen im Dialog "Lage der Instanzebene" ein. Die Felder bei "Position" bestimmen die Lage unseres Konstrukts im Raum in Abhängigkeit zum Nullpunkt ( x=0 /y=0 / z=0). Bei "Drehungen" können wir unserer geometrischen Figur Drehbefehle um die x,y und z-Achse geben. Das Feld Skalierung (vgl. englisch scale = Maßstab) bedeutet nichts anders, als das wir über diese Einstellungen Einfluß auf die Größe unseres Rechtecks in eben der x,y und z-Richtung in Abhängigkeit von unseren eingegebenen Grundmaßen geben können. Würden wir also hier bei Skalierung /z.B. die x-Skalierung = 0.5 setzen, würde sich unser Rechteck in den X-Maßen auf die Hälfte reduzieren - sprich bei dem von uns eingegebenen Grundmaß von 1200 cm auf nunmehr 600 cm. | + | Gehen wir nun etwas genauer auf die Einstellungen im Dialog "Lage der Instanzebene" ein. Die Felder bei "Position" bestimmen die Lage unseres Konstrukts im Raum in Abhängigkeit zum Nullpunkt ( x=0 /y=0 / z=0). Bei "Drehungen" können wir unserer geometrischen Figur Drehbefehle um die x,y und z-Achse geben. Das Feld Skalierung (vgl. englisch scale = Maßstab) bedeutet nichts anders, als das wir über diese Einstellungen Einfluß auf die Größe unseres Rechtecks in eben der x,y und z-Richtung in Abhängigkeit von unseren eingegebenen Grundmaßen geben können. Würden wir also hier bei Skalierung /z.B. die x-Skalierung = 0.5 setzen, würde sich unser Rechteck in den X-Maßen auf die Hälfte reduzieren - sprich bei dem von uns eingegebenen Grundmaß von 1200 cm auf nunmehr 600 cm. Das heißt, der hier eingegeben Wert verändert die Grundmaße unsere geometrischen Figur, indem er das Grundmaß mit dem eingegebenen Wert multipliziert. Bei der Skalierung sind Eingaben von 0 - 1000 möglich. |
<b><u>Position</u></b> | <b><u>Position</u></b> | ||
| Zeile 155: | Zeile 156: | ||
<b><u>Drehungen</u></b> | <b><u>Drehungen</u></b> | ||
| − | Durch die eingetragene Ausgangsdrehung von 270° wird unsere geometrische Figur senkrecht im Raum aufgerichtet. Das heißt alle unsere bis zu diesem Abschnitt des Handbuchs gezeichneten und im 3D-Betrachter sichtbar gemachten Konstrukte - wie z.B. das Rechteck und der Kreis - sind automatisch senkrecht im Raum aufgestellt worden. Dies ist bei der Erstellung eines Hauses sehr hilfreich, möchten wir doch, daß z.B. unsere Hauswände gleich richtig im Raum aufgerichtet sind. Wollen wir in unserem Haus nun z.B. einen Fußboden darstellen, würden wir die X-Drehung um 90° reduzieren. Denn wir möchten ja, | + | Durch die eingetragene Ausgangsdrehung von 270° wird unsere geometrische Figur senkrecht im Raum aufgerichtet. Das heißt alle unsere bis zu diesem Abschnitt des Handbuchs gezeichneten und im 3D-Betrachter sichtbar gemachten Konstrukte - wie z.B. das Rechteck und der Kreis - sind automatisch senkrecht im Raum aufgestellt worden. Dies ist bei der Erstellung eines Hauses sehr hilfreich, möchten wir doch, daß z.B. unsere Hauswände gleich richtig im Raum aufgerichtet sind. Wollen wir in unserem Haus nun z.B. einen Fußboden darstellen, würden wir die X-Drehung um 90° reduzieren. Denn wir möchten ja, dass der Fußboden waagerecht im Raum liegt. Das heißt wir bekommen 270° minus 90° = 180°. Diesen Wert geben wir sodann bei der X-Drehung ein und gehen anschließend auf die Schaltfläche "Ansicht aktualisieren". Nun werden wir im 3D-Betrachter feststellen, dass sich unsere geometrische Figur um minus 90° gedreht hat und sich waagerecht im Raum befindet. Analog zur X-Drehung können wir unserer geometrischen Figur auch Drehungen um die Y- und Z-Achse zuweisen. An dieser Stelle ist es am sinnvollsten sich eine einfache Figur zu erstellen und nacheinander Werte im Feld der X-/Y- und Z-Drehung einzugeben und sich das jeweilige Ergebnis im 3D-Betrachter anzusehen. |
<b><u>Skalierung</u></b> | <b><u>Skalierung</u></b> | ||
| − | Im Feld Skalierung bietet sich uns die Möglichkeit unser 2D-Konstrukt in Abhängigkeit der gezeichneten X,Y und Z-Ausmaße zu skalieren, | + | Im Feld Skalierung bietet sich uns die Möglichkeit unser 2D-Konstrukt in Abhängigkeit der gezeichneten X,Y und Z-Ausmaße zu skalieren, dass heißt zu verkleinern oder zu vergrößern. Haben wir wie im obigen Beispiel der "Lage der Instanzebene" Eintragungen von X-/Y-/Z-Skalierung = 1, so wird unser Konstrukt in der Größe dargestellt wie wir es in den Ausmaßen in der *.kon-Datei gezeichnet haben. Möchten wir das Konstrukt nun in X/Y oder Z-Richtung verkleinern, so geben wir Werte von 0-0.999(Periode) ein. Das Konstrukt verkleinert sich nun für die eingegebene Richtung auf den Wert X/Y/Z-Eingabewert x(mal) (0) bis (0.999[Periode]), d.h. bei einer Eingabe von z.B. 0.5, auf die Hälfte seiner gezeichneten Ausmaße. Wollen wir das Konstrukt in Abhängigkeit seiner gezeichneten Ausmaße vergrößern, geben wir in den entsprechenden Felder X/Y/Z ein Vielfaches ein, wie z.B. 1.5 - so vergrößert sich das Konstrukt um die Hälfte seines ursprünglichen Ausmasses. Das Limit bei der Vergrößerung liegt bei dem jeweils 1000-fachen. |
<b><u>Face-Culling</u></b> | <b><u>Face-Culling</u></b> | ||
| − | Der Instanzen-Dialog bietet uns neben den eben beschriebenen Drehbefehlen noch weitere entscheidende Möglichkeiten. So finden wir unter Anderem auch den Bereich des | + | Der Instanzen-Dialog bietet uns neben den eben beschriebenen Drehbefehlen noch weitere entscheidende Möglichkeiten. So finden wir unter Anderem auch den Bereich des [Face-Cullings]. Die englischen Begriffe sind hier am Besten mit "face" = "Fläche" und "culling" = "das Ausblenden" zu übersetzen. Bei dem Bereich des Face-Culling handelt es sich somit um die Möglichkeit Flächen unserer geometrischen Figur auszublenden. Die Einstellungen reichen hier von "Kein" über "Kein+Vorderseite", zu "Vorderseite" bis hin zu "Rückseite". Es stehen uns also vier Verfahren zur Verfügung, die wir auf unser Konstrukt anwenden können. Die klassische und auch grundlegende Einstellung ist das Ausblenden der Rückseite. Das Ausblenden von Flächen versetzt uns in die Lage, Flächen die später in unserem Modell nicht sichtbar sein müssen oder sein sollen von der Darstellung auszuschließen. Der Hintergrund dieses Verfahrens ist, daß durch das gezielte Ausblenden von Teilen eines Modells der spätere Rechenprozess - das sogenannte Rendering des Modells - im Programm so effektiv als möglich erfolgen kann. |
<b><u>Neue Instanzen /Kopien anlegen</u></b> | <b><u>Neue Instanzen /Kopien anlegen</u></b> | ||
| − | Eine weitere sehr wichtige Eigenschaft der Instanzenebene ist, | + | Eine weitere sehr wichtige Eigenschaft der Instanzenebene ist, dass sie uns in die Lage versetzt Kopien von unserer geometrischen Figur zu erstellen, d.h. wir haben die Möglichkeit unser gezeichnetes Konstrukt mehrfach im 3D-Raum zu platzieren. Dies erreichen wir indem wir im ersten Dialog der Instanzebene die Schaltfläche "Neue Instanz" auswählen. Haben wir dies getan können wir sogleich über "Gehe zu..." zu unserer neu angelegten Instanz gelangen. Neu angelegte Instanzen, die einer KON-Datei hinzugefügt werden, erhalten automatisch die Parameter der zuletzt aufgerufenen Instanz, d.h. die Position, die Drehung, die Skalierung und alle weiteren Einstellungen wie z.B. das [Face-Culling], die Ausleuchtung und das [Z-Offset]. Alle Parameter sind bei Aufruf der Instanz dann veränderbar. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <center>[[Datei:3.2.instanztebene-kopiendialog_1.jpg]]</center> | ||
| + | <b>Anbei ein anschauliches Beispiel für den Einsatz mehrerer Instanzen:</b> | ||
| + | (Wir sehen hier eine .kon einer Inneneinrichtung eines Triebwagens. Die .kon-Datei hat 20 Instanzen. Als Beispiel sind die Instanzen 0 und 1 mit ihren Einstellungen gezeigt) | ||
| + | <center>[[Datei:3.2.instanztebene-kopiendialog-2d-bsp-a-reduced.jpg]]</center> | ||
| + | <b>...und in der 3D-Ansicht</b> | ||
| + | <center>[[Datei:3.2.instanztebene-kopiendialog-3d-bsp.jpg]]</center> | ||
[http://wiki.eepshopping.de/index.php?title=Hauptseite_EEP_Wiki&redirect=no Zurück zur Startseite] | [http://wiki.eepshopping.de/index.php?title=Hauptseite_EEP_Wiki&redirect=no Zurück zur Startseite] | ||
Aktuelle Version vom 27. April 2017, 15:51 Uhr
Haben wir unser neu erstelltes Objekt aufgerufen und ist es aktiv wollen wir in das Modellieren selbst einsteigen. Ein Objekt besteht immer aus einer Untergruppe von sogenannten .kon-Dateien. Dies sind 2D Konstruktionsdateien, in welchen wir die Geometrie des Objektes zeichnen. Eine neue *.kon-Datei legen wir an, indem wir auf das Symbol ![]() auf unserer oberen Schaltfläche klicken.Es erscheint ein Fenster mit einem roten Koordinatensystem und der Bezeichnung unseres Objektnamens mit dem Zusatz „…-Kon_001.kon“. Wir maximieren uns das Fenster um nun mit mehr Übersicht arbeiten zu können.
auf unserer oberen Schaltfläche klicken.Es erscheint ein Fenster mit einem roten Koordinatensystem und der Bezeichnung unseres Objektnamens mit dem Zusatz „…-Kon_001.kon“. Wir maximieren uns das Fenster um nun mit mehr Übersicht arbeiten zu können.
Die KON-Datei ist für uns am Anfang das wichtigste Element für die Konstruktion von Modellen. Hier zeichnen wir die darzustellenden Flächen und legen ihre Position im 3D Raum fest. Wichtig ist, das wir immer geschlossene Formen zeichnen, und gewisse Regeln einhalten.
Sobald wir eine *.kon erstellt oder geöffnet haben, stehen uns folgende Zeichenwerkzeuge und Funktionsschaltflächen zur Verfügung.
Die Schaltflächen/Zeichenwerkzeuge im einzelnen:
![]() schneidet markierte Bereiche aus, gespeichert in der Zwischenablage
schneidet markierte Bereiche aus, gespeichert in der Zwischenablage
![]() kopiert markierte Bereiche in die Zwischenablage
kopiert markierte Bereiche in die Zwischenablage
![]() fügt Inhalte der Zwischenablage in aktive Kon-Datei ein (an selber Position wie im Original)
fügt Inhalte der Zwischenablage in aktive Kon-Datei ein (an selber Position wie im Original)
![]() zeichnet Unterteilungs- /Verbindungslinien
zeichnet Unterteilungs- /Verbindungslinien
![]() zeichnet Aussenkanten und Ausschlusslinien von Modellteilen
zeichnet Aussenkanten und Ausschlusslinien von Modellteilen
![]() zeichnet einzelne Vertexe
zeichnet einzelne Vertexe
![]() zeichnet Rechteck mit Aufruf eines Dialogs
zeichnet Rechteck mit Aufruf eines Dialogs
![]() zeichnet Ellipse mit Aufruf eines Dialogs
zeichnet Ellipse mit Aufruf eines Dialogs
![]() Werkzeug zum Löschen von Linien und Vertexen
Werkzeug zum Löschen von Linien und Vertexen
![]() blendet das Lineal ein und aus
blendet das Lineal ein und aus
![]() legt die Skala des Lineals auf die andere Seite
legt die Skala des Lineals auf die andere Seite
![]() verschiebt ausgewählten Vertex
verschiebt ausgewählten Vertex
![]() verbindet Linien
verbindet Linien
![]() ruft den Dialog "Eigenschaften von Vertex" auf
ruft den Dialog "Eigenschaften von Vertex" auf
![]() ruft den Instanzendialog auf
ruft den Instanzendialog auf
![]() farbbestimmender Vertex
farbbestimmender Vertex
![]() ruft den Dialog zum Hinzufügen einer neuen Textur auf
ruft den Dialog zum Hinzufügen einer neuen Textur auf
![]() überträgt die Farbwerte des zuletzt bearbeiteten Vertex auf weitere
überträgt die Farbwerte des zuletzt bearbeiteten Vertex auf weitere
![]() überträgt die Lichtwerte des zuletzt bearbeiteten Vertex auf weitere
überträgt die Lichtwerte des zuletzt bearbeiteten Vertex auf weitere
![]() überträgt die Höhenwerte (Z) des zuletzt bearbeiteten Vertex auf weitere
überträgt die Höhenwerte (Z) des zuletzt bearbeiteten Vertex auf weitere
![]() Vertex Datenwert(Nur die ID?)
Vertex Datenwert(Nur die ID?)
![]() Kon-Datei einbauen
Kon-Datei einbauen
![]() vergrößert die Darstellung
vergrößert die Darstellung
![]() verkleinert die Darstellung
verkleinert die Darstellung
![]() markiert einen Bereich zum Ausschneiden, Kopieren, Löschen oder Manipulation
markiert einen Bereich zum Ausschneiden, Kopieren, Löschen oder Manipulation
![]() zum rückgängig machen von Aktionen
zum rückgängig machen von Aktionen
![]() Stellt rückgängig gemachte Aktionen wieder her
Stellt rückgängig gemachte Aktionen wieder her
3.1 Zeichnen geometrischer Figuren
In der unteren Schaltfläche sehen wir wie oben beschrieben nebeneinander angeordnet unsere Zeichenwerkzeuge – beginnend mit einer gestrichelten, weiter mit einer durchgezogenen Linie, gefolgt von Einzelpunkten etc. Diese Werkzeuge ermöglichen es uns nun geometrische Figuren in unserem Koordinatensystem zu zeichnen.
3.1.1 Rechteck
Wir beginnen mit einer einfachen geometrischen Figur dem Rechteck, und klicken hierfür auf die Schaltfläche mit dem Symbol ![]() . An unserem Mauszeiger öffnet sich ein offenes Rechtecksymbol. Dies zeigt uns an, dass wir nun mit dem Zeichen beginnen können und wir tun dies gleich, indem wir nach einem Druck auf die linke Maustaste (LMT) das Rechteck beliebig nach allen Seiten im Koordinatensystem aufziehen.
. An unserem Mauszeiger öffnet sich ein offenes Rechtecksymbol. Dies zeigt uns an, dass wir nun mit dem Zeichen beginnen können und wir tun dies gleich, indem wir nach einem Druck auf die linke Maustaste (LMT) das Rechteck beliebig nach allen Seiten im Koordinatensystem aufziehen.
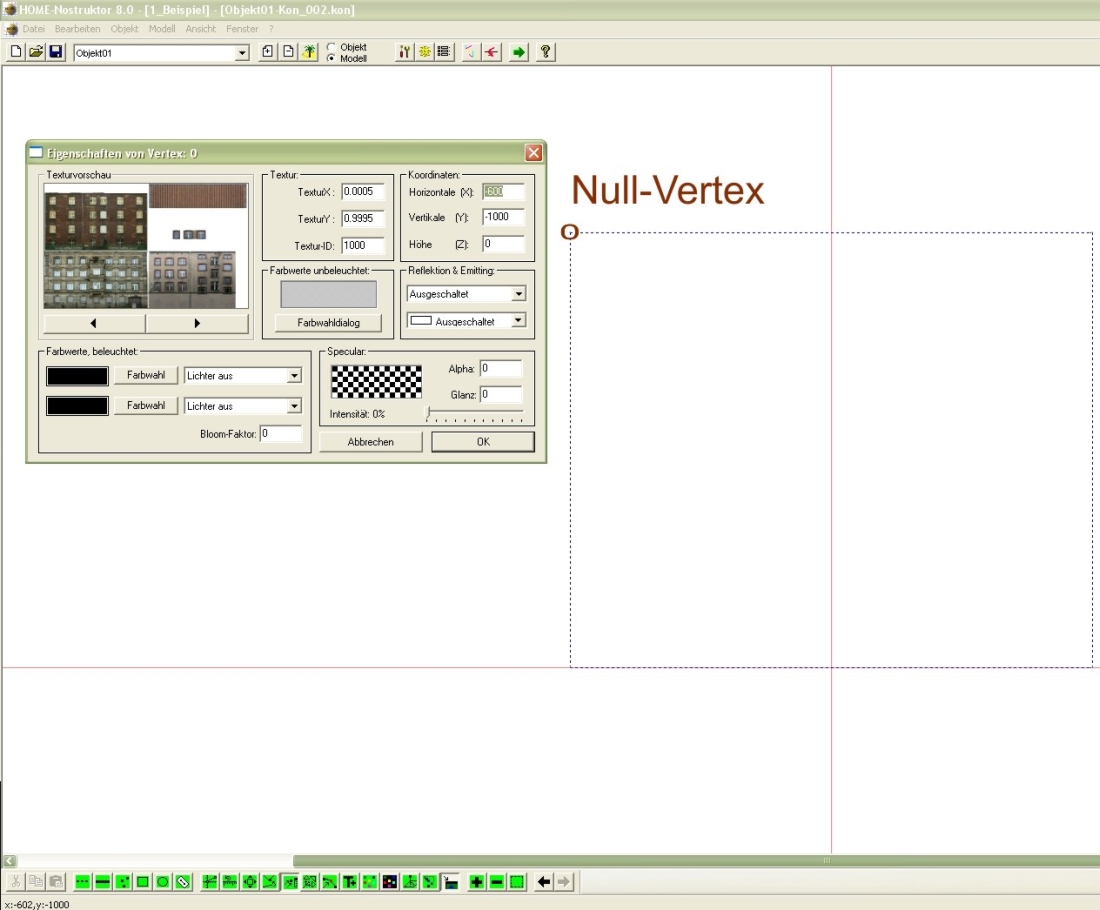
Es erscheint der Dialog für die geometrische Figur des Rechtecks:
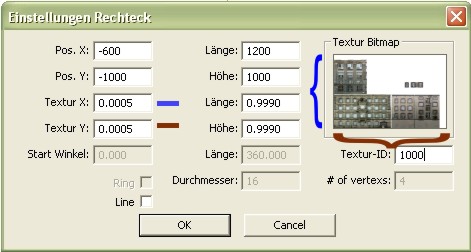
Die Pos.X und Pos.Y (Pos.=Position) bestimmen die Lage unserer geometrischen Figur in Abhängigkeit zum Nullpunkt (x=0 /y=0) unseres Koordinatensystems. Im Falle des Rechtecks beziehen sich die dortigen Eingaben auf den linken oberen Punkt, den sogenannten Null-Vertex (oder auch Nullpunkt) unserer geometrischen Figur. In den Eingabefeldern Länge und Höhe definieren wir die Ausmaße unseres Rechtecks. Im oberen Beispiel erkennen wir die Eingaben Länge=1200 und Höhe=1000. Da die Eingaben in der Maßeinheit Zentimeter erkannt werden, erhalten wir somit ein Rechteck mit einer Länge von 12 Metern und einer Höhe von 10 Metern. Die Eingabefelder Textur X/Y und die zugehörigen Felder Länge und Höhe geben uns die Möglichkeit unsere erstellten Texturen/Bilddateien auf unserer geometrische Figur aufzubringen. Im Feld Textur-ID tragen wir die entsprechende Nummer bzw. id der Textur ein, welche wir später auf unser Konstrukt aufbringen möchte.
Bestätigen wir unsere Eingaben mit OK erhalten wir folgende geometrische Figur. Zusätzlich öffnen wir in der Ansicht mit einem Doppelklick des Buttons ![]() auf den linken oberen Punkt unseren sogenannten Vertex-Dialog für eben den oberen linken Punkt (Vertex). Abgebildet sehen wir den Dialog in der oberen Grafik unter "Eigenschaften von Vertex:0". Wie wir an den Eigenschaften des Vertex(e) erkennen können hat unser Rechteck genau die vorher im Dialog eingestellten Ausmaße. Der bereits aufgerufenen Null-Vertex liegt in der Horizontale bei x=600 und in der Vertikale bei Y=-1000. Analog dazu werden wir beim Aufrufen der Eigenschaften des rechten, oberen Vertex die Koordinaten x=-600 und y=-1000 vergeben sehen. Die beiden unteren Vertexe liegen auf der X-Achse und haben somit beide die y-Werte = 0. In x-Ausrichtung sehen wir analog zu den beiden oberen Vertexen die Werte x=600 und x=-600. Dank der beiden Eingaben der Pos.X = -600 und der Pos.Y =-1000 liegt unser Rechteck in der Mitte der x-Achse und mit den beiden unteren Vertexen auf der y-Achse auf. (vgl. Pos.X/ Pos.Y in "Einstellung Rechteck")
auf den linken oberen Punkt unseren sogenannten Vertex-Dialog für eben den oberen linken Punkt (Vertex). Abgebildet sehen wir den Dialog in der oberen Grafik unter "Eigenschaften von Vertex:0". Wie wir an den Eigenschaften des Vertex(e) erkennen können hat unser Rechteck genau die vorher im Dialog eingestellten Ausmaße. Der bereits aufgerufenen Null-Vertex liegt in der Horizontale bei x=600 und in der Vertikale bei Y=-1000. Analog dazu werden wir beim Aufrufen der Eigenschaften des rechten, oberen Vertex die Koordinaten x=-600 und y=-1000 vergeben sehen. Die beiden unteren Vertexe liegen auf der X-Achse und haben somit beide die y-Werte = 0. In x-Ausrichtung sehen wir analog zu den beiden oberen Vertexen die Werte x=600 und x=-600. Dank der beiden Eingaben der Pos.X = -600 und der Pos.Y =-1000 liegt unser Rechteck in der Mitte der x-Achse und mit den beiden unteren Vertexen auf der y-Achse auf. (vgl. Pos.X/ Pos.Y in "Einstellung Rechteck")
Im 3D-Betrachter erhalten wir zu unserem Rechteck folgende Ansicht:
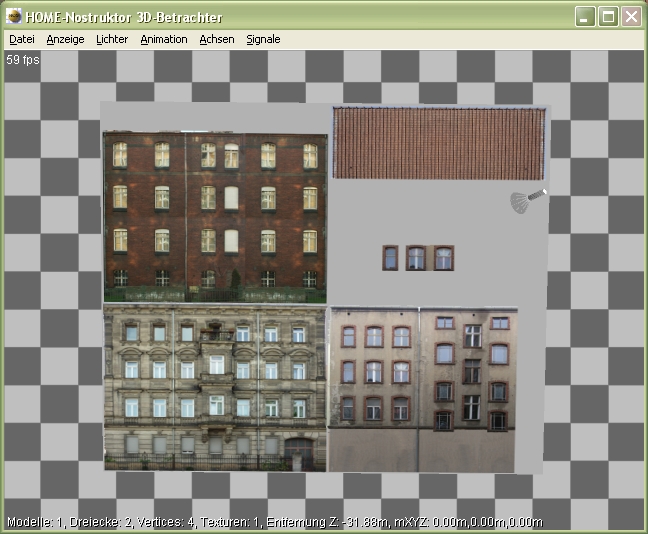
Nun lassen sich unsere Eingaben im Rechteckdialog anschaulich nachvollziehen. Wir erkennen, daß auf unserem Rechteck aktuell die gesamte Textur von x=0 (genau:0.0005) bis x=1 (0.9990)und von y=0 (genau:0.0005) bis y=1 (0.9990) aufgetragen ist.(vgl. hierzu "Einstellung Rechteck" Textur x/y, Länge/Höhe). Die genauen Werte sind an dieser Stelle wichtig, da wir ein Textur niemals direkt bis an Ihren Rand auftragen sollten.Würden wir dies tun entstünden an den Rändern unseres Rechtecks weiße, untexturierte Flächen. Die Informationen am unteren Rand unseres 3-D Betrachters liefern uns die aktuelle Anzahl an Dreiecken (in diesem Fall 2). Denn Zeichnen wir ein geometrische Figur wie hier das Rechteck, wird es uns auch als Rechteck dargestellt, intern allerdings immer in die kleinste geometrische Einheit - d.h in Dreiecke aufgeteilt. Weiter wird uns die Anzahl an Vertexen/ Einzelpunkten = 4 angezeigt und die Anzahl an bereits verwendeten Texturen für unser Modell (aktuell = 1). Die Entfernungswerte informieren uns immer über den aktuellen Sichtabstand in unserer 3D-Ansicht.
3.1.2. Kreise, Ellipsen und Linien
Wie für unser Rechteck haben wir in den Zeichenwerkzeugen auch Schaltflächen für die Zeichnung von Kreisen, Ellipsen und Linien. Für die Erstellung eines Kreises oder einer Ellipse verwenden wir die Schaltfläche ![]() . Wie bei dem Dialog "Einstellung Rechteck" haben wir hier die Möglichkeit die Position, die Größe und die Parameter für das Auftragen der Textur einzugeben. Möchten wir einen Kreis zeichnen geben wir in den Feldern Länge und Höhe identische Werte ein. Soll eine Ellipse gezeichnet werden geben wir die jeweils gewünschte Ausdehnung in Länge und Höhe ein. Ebenfalls entscheidend für die Erstellung eines Kreises bzw. einer Ellipse ist die Eingabe der Anzahl der Vertexe. (vgl. hierzu: "# of vertexs: ..." in den Einstellungen / in unserem Bsp. ist der Wert = 18 ). Das heißt wir bekommen einen Kreis, der aus 18 einzelnen Dreiecken besteht.
. Wie bei dem Dialog "Einstellung Rechteck" haben wir hier die Möglichkeit die Position, die Größe und die Parameter für das Auftragen der Textur einzugeben. Möchten wir einen Kreis zeichnen geben wir in den Feldern Länge und Höhe identische Werte ein. Soll eine Ellipse gezeichnet werden geben wir die jeweils gewünschte Ausdehnung in Länge und Höhe ein. Ebenfalls entscheidend für die Erstellung eines Kreises bzw. einer Ellipse ist die Eingabe der Anzahl der Vertexe. (vgl. hierzu: "# of vertexs: ..." in den Einstellungen / in unserem Bsp. ist der Wert = 18 ). Das heißt wir bekommen einen Kreis, der aus 18 einzelnen Dreiecken besteht.
Möchten wir eine Verbindungs- bzw. Unterteilungslinie zeichnen verwenden wir die Schaltfläche ![]() . Bei der Linie ist zu beachten, daß sie keine eigenen Vertexe/Punkte enthält. Sie dient lediglich zur Verbindung zweier Vertexe. Hierzu mehr im Abschnitt "3.1.3 Vertexe/Punkte zeichnen und Vertexeigenschaften".
. Bei der Linie ist zu beachten, daß sie keine eigenen Vertexe/Punkte enthält. Sie dient lediglich zur Verbindung zweier Vertexe. Hierzu mehr im Abschnitt "3.1.3 Vertexe/Punkte zeichnen und Vertexeigenschaften".
In der 2D Ansicht erhalten wir nun für einen Kreis folgende Darstellung:
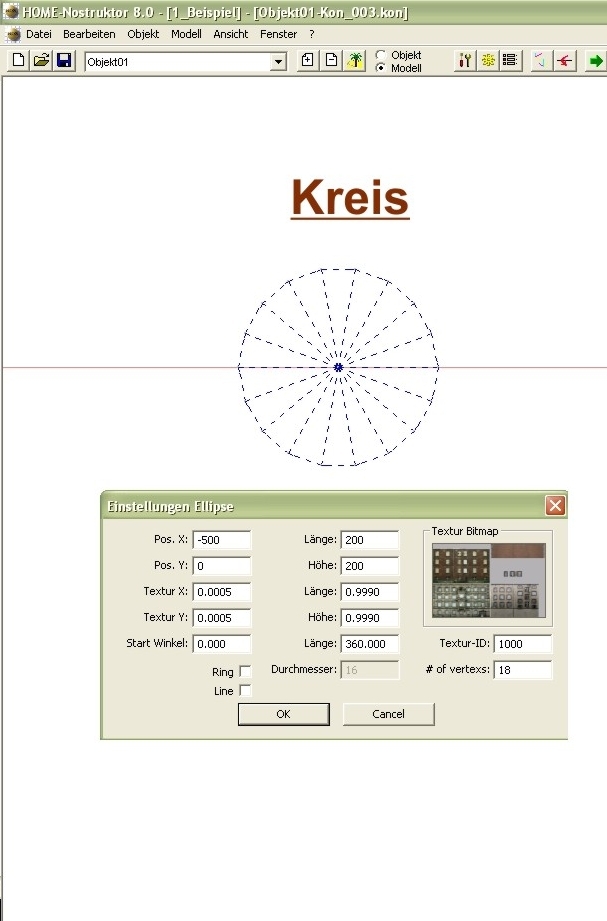
und folgende Darstellung für eine Ellipse bzw. Linie:
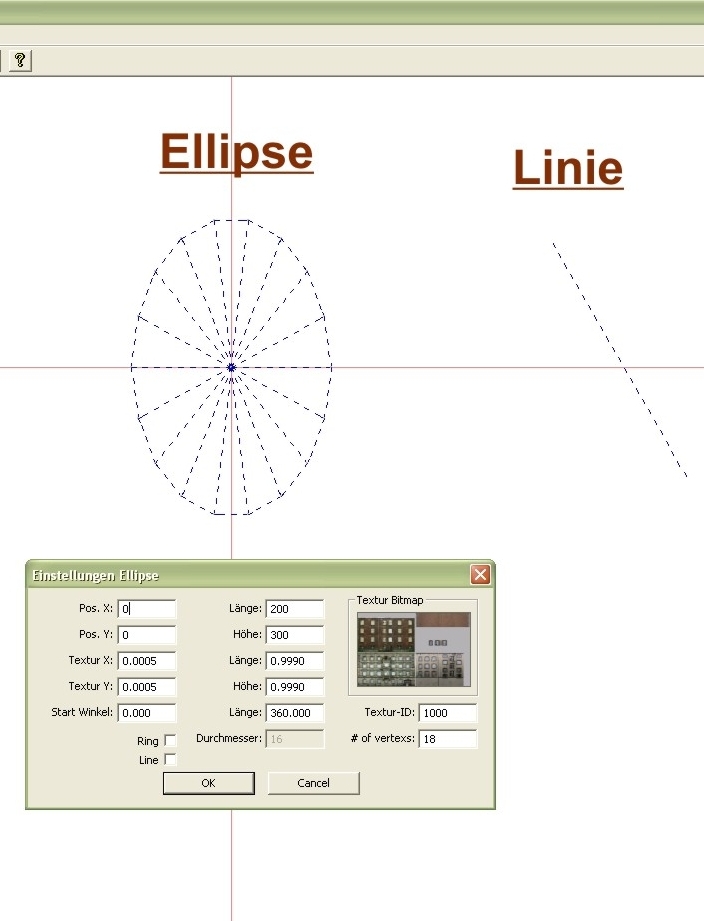
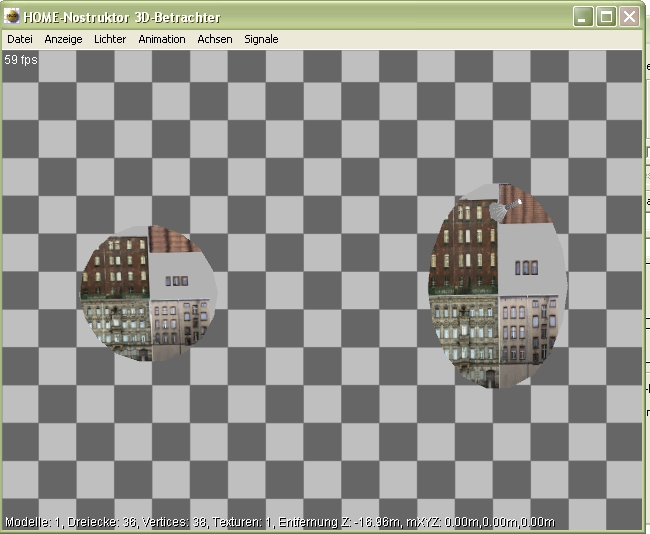
Und hier unsere 2D-Zeichnung im 3D-Betrachter. Wir erkennen unseren Kreis und die Ellipse. Und bemerken, dass unsere Linie nicht sichtbar ist. Dies rührt daher, dass sie wie oben beschrieben über keine eigenen Einzelpunkte verfügt. Würde man unsere Linie nun nachträglich mit Vertexen/Punkten versehen, erhielten wir allerdings ebenfalls (noch) keine 3D Darstellung, da eine einfache Linie weder über eine 2D Fläche noch über ein 3D-Volumen verfügt.
3.1.3 Vertexe /Punkte zeichnen, Vertexeigenschaften
Ebenso wie wir Rechtecke, Kreise und Ellipsen zeichnen können, haben wir die Möglichkeit Einzelpunkte/Vertexe in unserem Koordinatensystem zu setzen. Sie dienen zum einen dazu vorab gezeichnete geometrische Figuren zu ergänzen. Zum Anderen lassen sich mit ihnen aber auch eigene geometrische Figuren mit Hilfe der Verbindungs- /Unterteilungslinien erstellen. Einzelen Vertexe setzen wir über die Schaltfläche ![]() . Die Vertexe werden innerhalb des Zeichenrasters gesetzt. Mit den Verbindungslinien
. Die Vertexe werden innerhalb des Zeichenrasters gesetzt. Mit den Verbindungslinien ![]() verbinden wir nun unsere vorab gesetzten Einzelvertexe zu einer geometrischen Figur, wie im unteren Beispiel zu einem Dreieck.
verbinden wir nun unsere vorab gesetzten Einzelvertexe zu einer geometrischen Figur, wie im unteren Beispiel zu einem Dreieck.
Über den Vertexdialog ![]() lassen sich die Lage des Vertexes im Raum (Koordinaten x,y,z), seine Grundfarbe (Farbwerte unbelechtet), Lichteinstellungen (Farbwerte beleuchtet), die Reflektionseinstellungen (Reflektion&Emitting) und die spekularen Lichteinstellungen (Specular) setzen. Über den Bereich "Textur" im Vertexdialog haben wir die Möglichkeit die Lage des Vertexes auf unserer Textur in x und y Richtung zu bestimmen. Ferner haben wir die Möglichkeit ein Bloom-Faktor zu vergeben.
lassen sich die Lage des Vertexes im Raum (Koordinaten x,y,z), seine Grundfarbe (Farbwerte unbelechtet), Lichteinstellungen (Farbwerte beleuchtet), die Reflektionseinstellungen (Reflektion&Emitting) und die spekularen Lichteinstellungen (Specular) setzen. Über den Bereich "Textur" im Vertexdialog haben wir die Möglichkeit die Lage des Vertexes auf unserer Textur in x und y Richtung zu bestimmen. Ferner haben wir die Möglichkeit ein Bloom-Faktor zu vergeben.

In den Eigenschaften (Vertexdialog) unseres Punktes lassen sich sogleich folgende Einstellungen erkennen:
Wir sehen im Feld Koordinaten die Lage bei X=0 und y =-50, d.h. unser Vertex liegt auf dem Nullpunkt der Y-Achse und hat eine Lage von 50 Zentimeter oberhalb der X-Achse. Im Eingabefeld (Z) haben wir die Möglichkeit für den Punkt auch in der Z-Achse ( in diesem Fall Tiefe ) eine Lage zu bestimmen. Wir haben somit über die dritte Achse (z-Achse) in unserem Koordinatensystem die Möglichkeit unserer geometrischen Figur ein räumliches .......
Die Textur-ID ist in unserem Bsp. aktuell noch nicht gesetzt, d.h. es ist noch keine Textur/kein Bild ausgewählt welches wir auf unseren Punkt auftragen möchten. Der Standardwert ist hier deshalb noch bei -1. Bei den "Farbwerten unbeleuchtet" haben wir Möglichkeit unserem Vertex eine Grundfarbe im RGB-Farbspektrum zuzuteilen. Dies kann z.B. dann sinnvoll sein, wenn wir unsere Textur an dieser Stelle abdunkeln wollen - so würden wir z.B. einen Grauton als Grundfarbe hinterlegen. Aktuell sind unseren Vertexen in der Grafik rote Grundfarben zugewiesen. Wichtig in diesem Zusammenhang ist, daß wir die Farbwerte der Vertexe standardmäßig auf die RGB-Werte: 200-200-200 einstellen sollte.
Auf die Punkte der "Farbwerte beleuchtet", "Reflektion&Emitting" und "Specular" gehen wir in einem späteren Kapitel ein. Diese Einstellungen können für unser Modell auch nach der eigentlichen Konstruktionsarbeit gesetzt und vergeben werden.
Kommen wir nun aber zurück zur eigentlichen Konstruktionsarbeit mit Vertexen. Im oberen Schaubild sehen wir eine Dreieckskonstruktion. Diese geometrische Figur erstellen wir in dem wir 3 Einzelvertexe an unseren gewünschten Punkten im Koordinatensystem setzen und sie anschließend mit der ![]() Unterteilungs- /Verbindungslinie verbinden. Im 3D-Betrachter erhalten wir folgende Darstellung:
Unterteilungs- /Verbindungslinie verbinden. Im 3D-Betrachter erhalten wir folgende Darstellung:
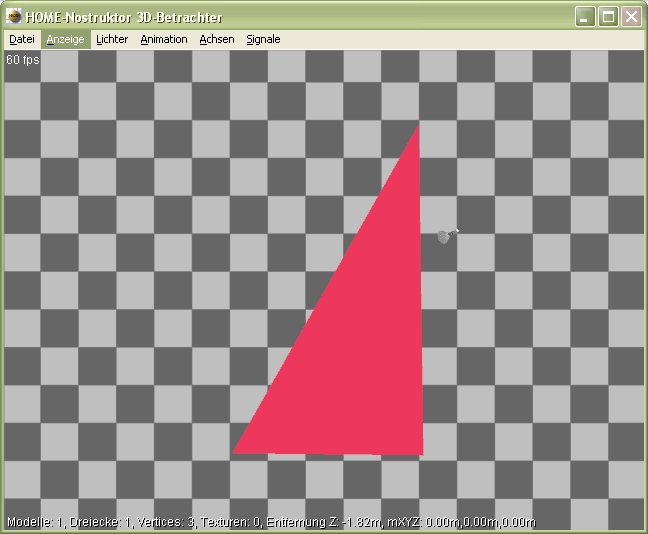
Diesmal haben wir - wie in den Eigenschaften unseres Vertex erkennbar - keine Textur-ID eingegeben und erhalten deshalb unser Dreieck mit den eingestellten Grundfarben "Farbwerte unbeleuchtet".
3.1.4. Arbeiten mit Ausschlusslinien
Um Flächen innerhalb einer geometrischen Figur auszuschneiden bzw. deren Darstellung auszuschließen setzen wir die sogenannte Ausschlusslinie ![]() ein. Wir stellen uns an dieser Stelle z.B. ein Fenster oder eine Tür vor, die geöffnet sein sollen - oder aber z.B einen Mauerdurchbruch, den wir darstellen möchten. Um dies in unserem Modelle darzustellen gehen wir wie folgt vor:
ein. Wir stellen uns an dieser Stelle z.B. ein Fenster oder eine Tür vor, die geöffnet sein sollen - oder aber z.B einen Mauerdurchbruch, den wir darstellen möchten. Um dies in unserem Modelle darzustellen gehen wir wie folgt vor:
Wir erstellen wie gewohnt unser gewünschtes Objekt, z.B. eine Hauswand über die Schaltfläche des Rechtecks. Im Bsp. des linken Rechtecks haben wir die Verbindungslinien verwendet. Im rechten haben wir Ausschlusslinien eingesetzt.
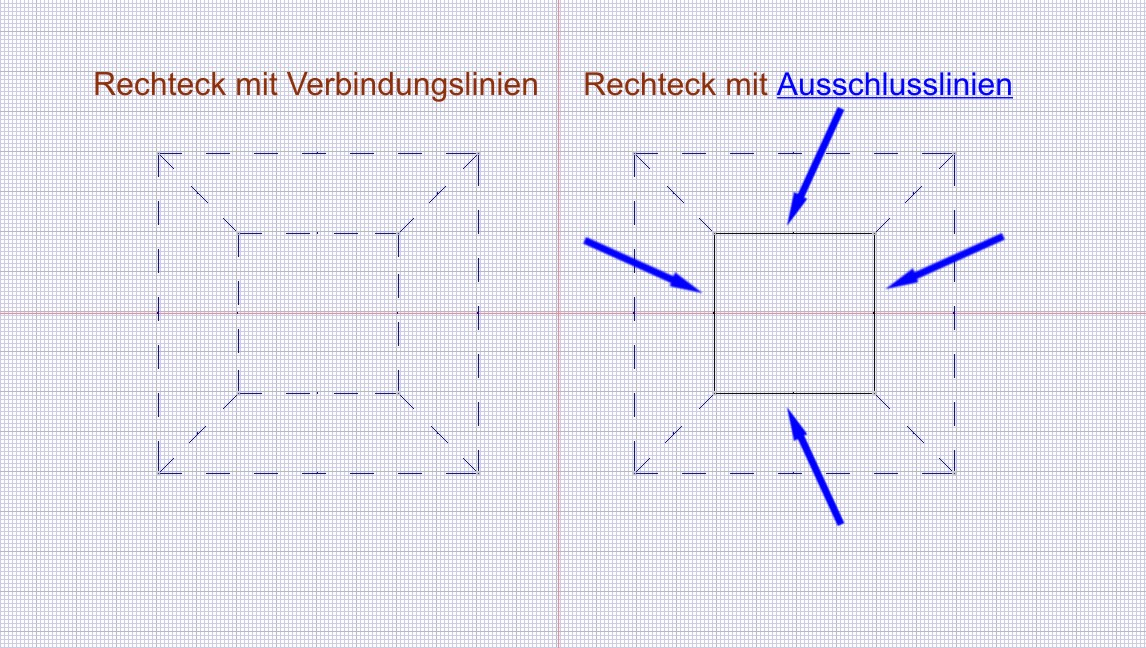
...in unserer 3D-Ansicht ist der Unterschied für uns sofort gut erkennbar:
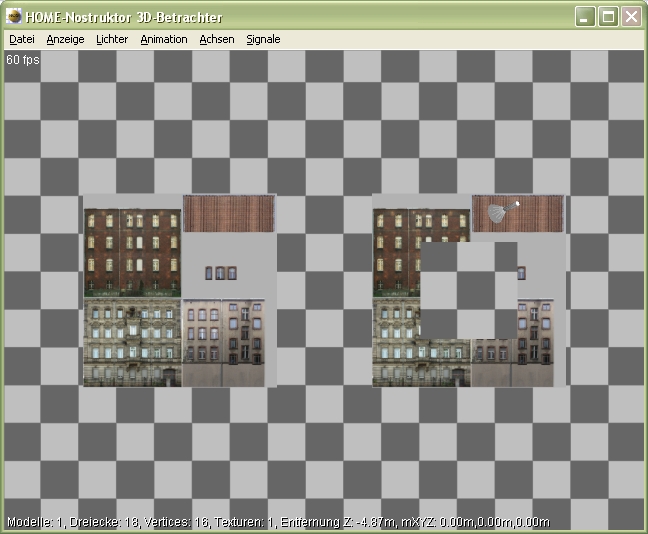
Abb.: Instanzebene der *.kon-Datei
3.2. Die Instanzebene unserer .kon-Datei
Alle erzeugten *.kon-Dateien verfügen über eine sogenannte Instanzebene. Bei der Neuerstellung erhält jede *.kon in ihrer Instanzebene automatisch eine Ausgangsdrehung um die X-Achse von 270°. Dies ist im Instanzen-Dialog rot markiert zu erkennen ist. Die Ausgangsdrehung stellt das Konstrukt somit automatisch in eine senkrechte Position in unserem Koordinatensystem.
Den Dialog jeder einzelnen *.kon-Datei rufen wir uns über das Symbol ![]() auf. Wir erhalten dann folgende Ansicht:
auf. Wir erhalten dann folgende Ansicht:
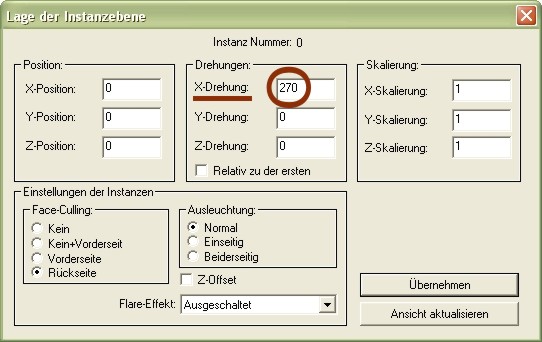
Abb.: Instanzebene der *.kon-Datei
3.2.1 Lage im Koordinatensystem
Nachfolgend sehen wir die Ausgangslage eines Konstrukts einer .kon-Datei im Koordinatensystem. Ausgangslage bedeutet, dass das Konstrukt nach Erstellung noch keine weiteren Parameter als die automatisch eingestellte Ausgangsdrehung erhalten hat. Die Ausgangsdrehung von 270° (= -90°) ist in der Grafik gut ersichtlich. Die Achse um die primär, neben der automatischen Aufstellung um die x-Achse von -90°/ 270°, gedreht wird ist die z-Achse. So würden z.B. die Seiten des in der Abbildung zu sehenden Hauses um -90° bzw. +90° um die z-Achse gedreht. Natürlich gibt es hier von Modell zu Modell Unterschiede. Als Ausgangspunkt ist es gut sich immer hier gezeigte Ausgangslage anzusehen bzw. vorzustellen, und von dort aus Schritt für Schritt die Drehungen um die x,y, und z-Achsen vorzunehmen, bis die gewünschten Lage des Konstrukts im Raum erreicht ist.
Siehe hierzu auch Kapitel: Normen und Maßvorgaben (Lage der Modelle)
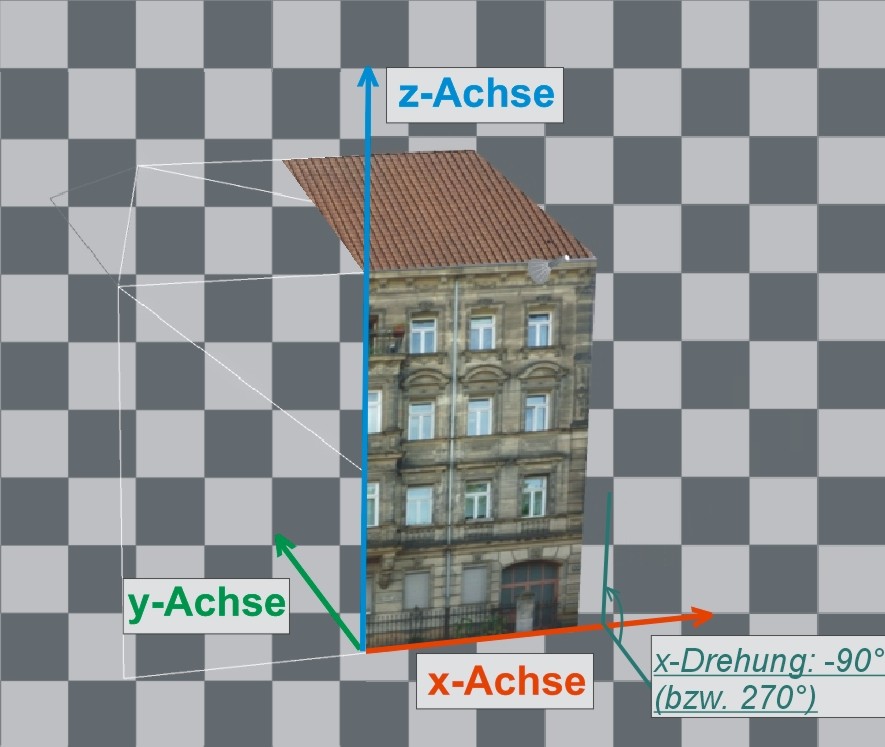
Abb.: 3D-Ansicht der Lage einer .kon-Datei mit Ausgangsdrehung 270° im Koordinatensystem
Erklärungen zu den Einstellungen in den Instanzen
Gehen wir nun etwas genauer auf die Einstellungen im Dialog "Lage der Instanzebene" ein. Die Felder bei "Position" bestimmen die Lage unseres Konstrukts im Raum in Abhängigkeit zum Nullpunkt ( x=0 /y=0 / z=0). Bei "Drehungen" können wir unserer geometrischen Figur Drehbefehle um die x,y und z-Achse geben. Das Feld Skalierung (vgl. englisch scale = Maßstab) bedeutet nichts anders, als das wir über diese Einstellungen Einfluß auf die Größe unseres Rechtecks in eben der x,y und z-Richtung in Abhängigkeit von unseren eingegebenen Grundmaßen geben können. Würden wir also hier bei Skalierung /z.B. die x-Skalierung = 0.5 setzen, würde sich unser Rechteck in den X-Maßen auf die Hälfte reduzieren - sprich bei dem von uns eingegebenen Grundmaß von 1200 cm auf nunmehr 600 cm. Das heißt, der hier eingegeben Wert verändert die Grundmaße unsere geometrischen Figur, indem er das Grundmaß mit dem eingegebenen Wert multipliziert. Bei der Skalierung sind Eingaben von 0 - 1000 möglich.
Position
Bestimmung der Lage des Konstrukts in Abhängigkeit zum Nullpunkt (x=0/y=0/z=0). Durch Eingabe von Werten in x,y,z legen wir somit den Abstand des Konstrukts von der jeweiligen x-,y-, und z-Achse fest.
Drehungen
Durch die eingetragene Ausgangsdrehung von 270° wird unsere geometrische Figur senkrecht im Raum aufgerichtet. Das heißt alle unsere bis zu diesem Abschnitt des Handbuchs gezeichneten und im 3D-Betrachter sichtbar gemachten Konstrukte - wie z.B. das Rechteck und der Kreis - sind automatisch senkrecht im Raum aufgestellt worden. Dies ist bei der Erstellung eines Hauses sehr hilfreich, möchten wir doch, daß z.B. unsere Hauswände gleich richtig im Raum aufgerichtet sind. Wollen wir in unserem Haus nun z.B. einen Fußboden darstellen, würden wir die X-Drehung um 90° reduzieren. Denn wir möchten ja, dass der Fußboden waagerecht im Raum liegt. Das heißt wir bekommen 270° minus 90° = 180°. Diesen Wert geben wir sodann bei der X-Drehung ein und gehen anschließend auf die Schaltfläche "Ansicht aktualisieren". Nun werden wir im 3D-Betrachter feststellen, dass sich unsere geometrische Figur um minus 90° gedreht hat und sich waagerecht im Raum befindet. Analog zur X-Drehung können wir unserer geometrischen Figur auch Drehungen um die Y- und Z-Achse zuweisen. An dieser Stelle ist es am sinnvollsten sich eine einfache Figur zu erstellen und nacheinander Werte im Feld der X-/Y- und Z-Drehung einzugeben und sich das jeweilige Ergebnis im 3D-Betrachter anzusehen.
Skalierung
Im Feld Skalierung bietet sich uns die Möglichkeit unser 2D-Konstrukt in Abhängigkeit der gezeichneten X,Y und Z-Ausmaße zu skalieren, dass heißt zu verkleinern oder zu vergrößern. Haben wir wie im obigen Beispiel der "Lage der Instanzebene" Eintragungen von X-/Y-/Z-Skalierung = 1, so wird unser Konstrukt in der Größe dargestellt wie wir es in den Ausmaßen in der *.kon-Datei gezeichnet haben. Möchten wir das Konstrukt nun in X/Y oder Z-Richtung verkleinern, so geben wir Werte von 0-0.999(Periode) ein. Das Konstrukt verkleinert sich nun für die eingegebene Richtung auf den Wert X/Y/Z-Eingabewert x(mal) (0) bis (0.999[Periode]), d.h. bei einer Eingabe von z.B. 0.5, auf die Hälfte seiner gezeichneten Ausmaße. Wollen wir das Konstrukt in Abhängigkeit seiner gezeichneten Ausmaße vergrößern, geben wir in den entsprechenden Felder X/Y/Z ein Vielfaches ein, wie z.B. 1.5 - so vergrößert sich das Konstrukt um die Hälfte seines ursprünglichen Ausmasses. Das Limit bei der Vergrößerung liegt bei dem jeweils 1000-fachen.
Face-Culling
Der Instanzen-Dialog bietet uns neben den eben beschriebenen Drehbefehlen noch weitere entscheidende Möglichkeiten. So finden wir unter Anderem auch den Bereich des [Face-Cullings]. Die englischen Begriffe sind hier am Besten mit "face" = "Fläche" und "culling" = "das Ausblenden" zu übersetzen. Bei dem Bereich des Face-Culling handelt es sich somit um die Möglichkeit Flächen unserer geometrischen Figur auszublenden. Die Einstellungen reichen hier von "Kein" über "Kein+Vorderseite", zu "Vorderseite" bis hin zu "Rückseite". Es stehen uns also vier Verfahren zur Verfügung, die wir auf unser Konstrukt anwenden können. Die klassische und auch grundlegende Einstellung ist das Ausblenden der Rückseite. Das Ausblenden von Flächen versetzt uns in die Lage, Flächen die später in unserem Modell nicht sichtbar sein müssen oder sein sollen von der Darstellung auszuschließen. Der Hintergrund dieses Verfahrens ist, daß durch das gezielte Ausblenden von Teilen eines Modells der spätere Rechenprozess - das sogenannte Rendering des Modells - im Programm so effektiv als möglich erfolgen kann.
Neue Instanzen /Kopien anlegen
Eine weitere sehr wichtige Eigenschaft der Instanzenebene ist, dass sie uns in die Lage versetzt Kopien von unserer geometrischen Figur zu erstellen, d.h. wir haben die Möglichkeit unser gezeichnetes Konstrukt mehrfach im 3D-Raum zu platzieren. Dies erreichen wir indem wir im ersten Dialog der Instanzebene die Schaltfläche "Neue Instanz" auswählen. Haben wir dies getan können wir sogleich über "Gehe zu..." zu unserer neu angelegten Instanz gelangen. Neu angelegte Instanzen, die einer KON-Datei hinzugefügt werden, erhalten automatisch die Parameter der zuletzt aufgerufenen Instanz, d.h. die Position, die Drehung, die Skalierung und alle weiteren Einstellungen wie z.B. das [Face-Culling], die Ausleuchtung und das [Z-Offset]. Alle Parameter sind bei Aufruf der Instanz dann veränderbar.
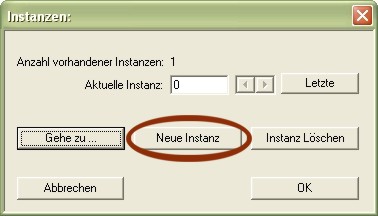
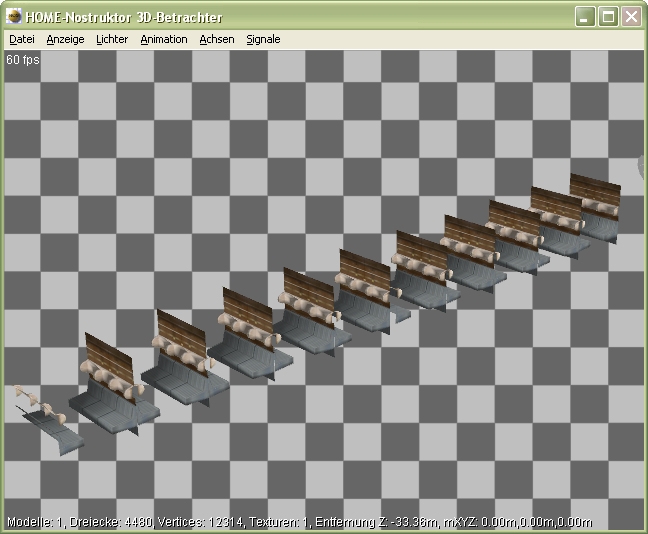
Anbei ein anschauliches Beispiel für den Einsatz mehrerer Instanzen:
(Wir sehen hier eine .kon einer Inneneinrichtung eines Triebwagens. Die .kon-Datei hat 20 Instanzen. Als Beispiel sind die Instanzen 0 und 1 mit ihren Einstellungen gezeigt)
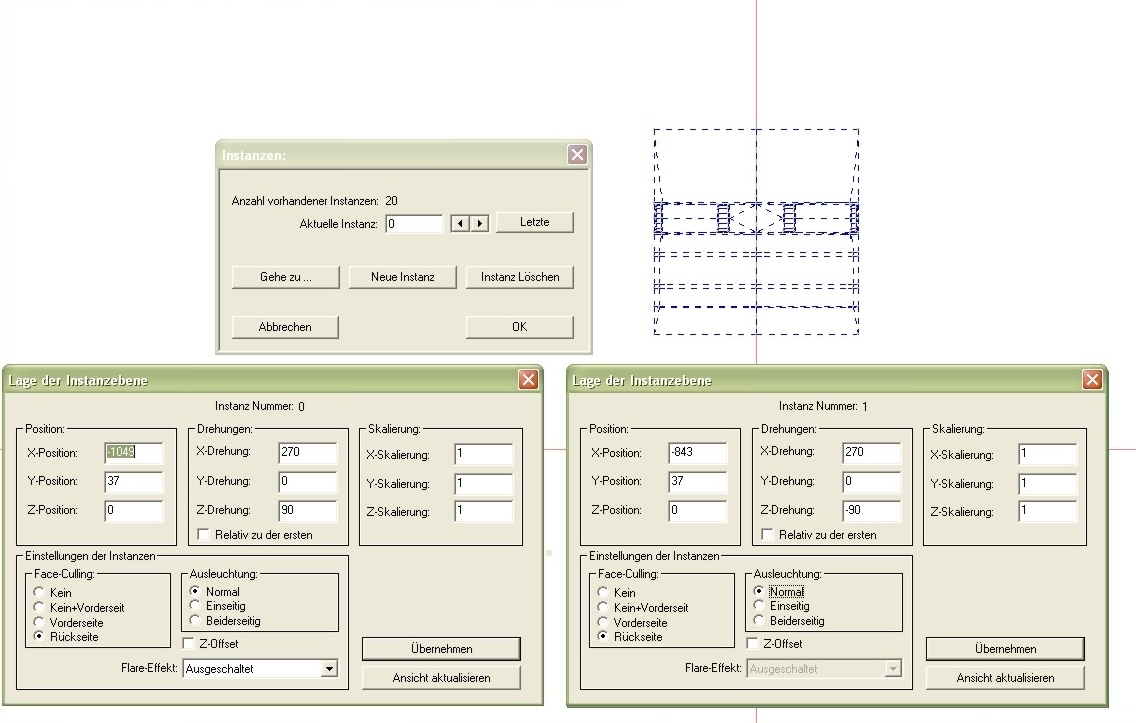
...und in der 3D-Ansicht