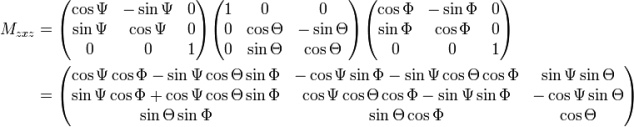O
OBJ (*.obj) = Objekt
Text
Orientierung
Orientierung ist ein Begriff aus der linearen Algebra und der Differentialgeometrie. In einem n-dimensionalen Raum haben zwei Basen die gleiche Orientierung, wenn sie durch lineare Abbildungen mit positiver Determinante (zum Beispiel Streckungen und Drehungen) auseinander hervorgehen. Sind zusätzlich Spiegelungen erforderlich, so ist die Determinante negativ und die Basen sind nicht gleich orientiert. Anschaulich gibt es zwei mögliche Orientierungen, ein Wechsel zwischen den Orientierungen ist durch Drehungen nicht möglich.
Beispiele: Spiegelschrift hat eine andere Orientierung als Schrift.
Schrauben mit Rechtsgewinde haben eine andere Orientierung als Schrauben mit Linksgewinde.
Eulersche Winkel oder auch Eulerwinkel sind eine Möglichkeit zur Beschreibung der Orientierung (Winkellage) von Objekten im dreidimensionalen Raum. Es handelt sich um drei Winkel, welche jeweils eine Drehung (Rotation) um bestimmte Achsen beschreiben und so eine Transformation zwischen zwei (kartesischen) Koordinatensystemen, dem Laborsystem und dem körperfesten System, definieren. Es existieren verschiedene Definitionen für die Eulerwinkel, die sich in der Wahl der Drehachsen unterscheiden. Von insgesamt 12 gleichwertigen möglichen Beschreibungen haben sich die unten angegebenen etabliert. Die angegebenen zugehörigen Drehmatrizen transformieren die Koordinaten des Körpers, der rotiert wird.
- •x-Konvention (Z, X’, Z’’)
- Zuerst wird um einen Winkel Ψ um die z-Achse des globalen Koordinatensystems (Z) gedreht. Es folgt eine Rotation um den Winkel Θ um die neue x-Achse (X’) und schließlich um den Winkel Φ um die nach den beiden vorherigen
Drehungen erhaltene z-Achse Z’’.
- •y-Konvention (Z, Y’, Z’’)
- Zuerst wird um einen Winkel Ψ um die z-Achse des globalen Koordinatensystems (Z) gedreht. Es folgt eine Rotation um den Winkel Θ um die neue y-Achse (Y’) und schließlich um den Winkel Φ um die nach den beiden vorherigen
Drehungen erhaltene z-Achse Z’’.
Da die resultierenden Matrizen Rotationsmatrizen sind, wird die Rücktransformation durch die Transponierte dargestellt.